Momentum Exchange

Learning Objectives

• Describe forces that deform surface objects and air parcels.
• Explain how momentum is exchanged in the ABL.
• Describe and quantify momentum transfer in the ABL.

Bed load movement and sediment transport is a function of Shear Stress.

Motivation

Atmospheric motions create forces that deform the atmosphere itself, deform and damage objects, and create waves on water surfaces.

Photo: A. Christen

Momentum exchange in the atmosphere, which is key to later understand and predict wind near the surface. The force exerted on the surface by the air being dragged over it is called the surface shearing stress (t ) and is expressed as a pressure (Pa, force per unit surface area).

What is Momentum? (iClicker)

Which would best describe momentum?

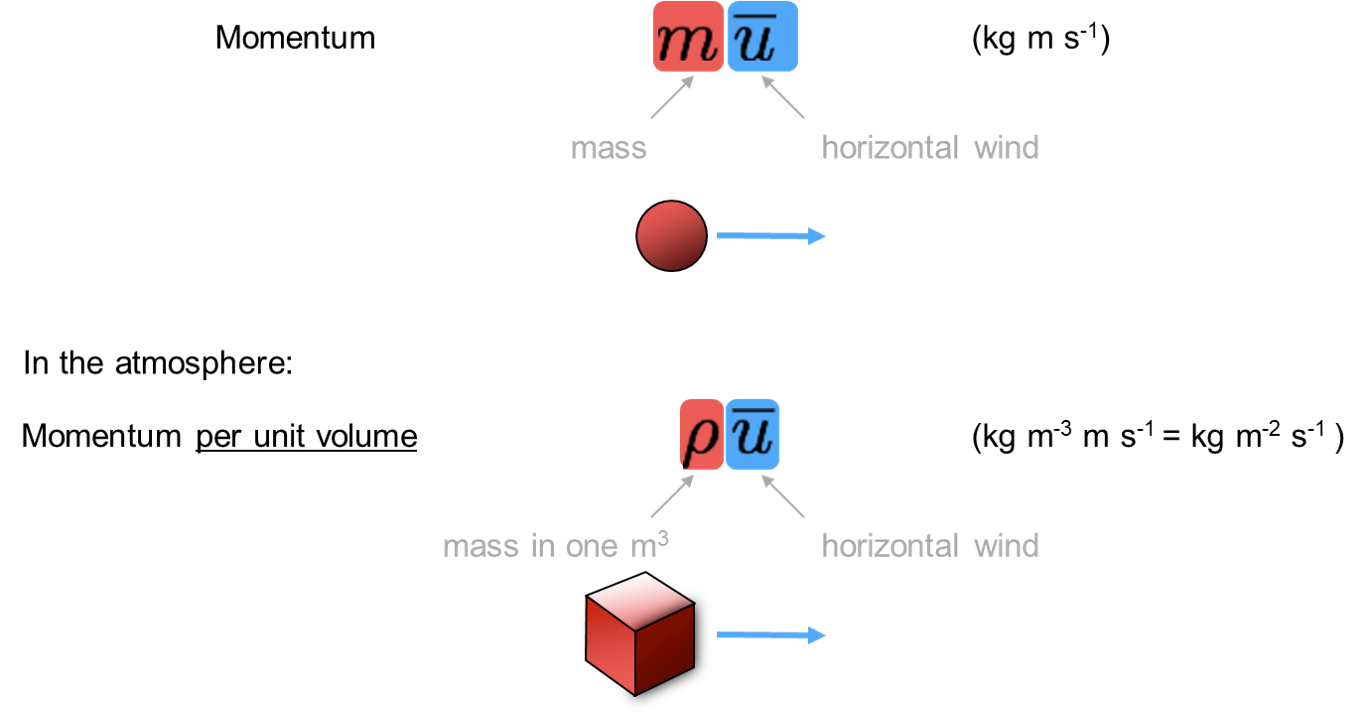
• A: Momentum = mass \(\times\) velocity
• B: Momentum = mass \(\times\) speed
• C: Momentum = mass \(\times\) direction
• D: Momentum = mass \(\times\) acceleration

Mechanics review -

The momentum a body is given by the product of its mass and velocity. In the case of the atmosphere the mean horizontal momentum of a unit volume is therefore given by its density (ρ) multiplied by its mean horizontal wind. Remember we use the overbar to

Source

LiveSlide Site https://www.windytv.com/?55.249,-121.536,4

Drag

In the ABL drag acts as an opposing force exerted by the surface, slowing wind.

• The drag force can be caused by form drag and skin drag.
• For a fluid to move, we require a horizontal force in the direction of the mean flow. Usually this is the pressure gradient force.

The wind speed in the planetary boundary layer is largely controlled by the frictional drag imposed on the flow by the underlying rigid surface. The drag retards motion close to the ground and gives rise to a sharp decrease of mean horizontal wind speed (u) as the surface is approached. The force exerted on the surface by the air being dragged over it is called the surface shearing stress (⌧ ) and is expressed as a pressure (Pa, force per unit surface area).

The wind speed in the atmospheric boundary layer is largely controlled by the fric- tional drag imposed on the flow by the underlying rigid surface.

Above the laminar boundary layer, in turbulent flows the ‘no-slip condition’ applies and the flow is brought to a standstill at the boundary.

Stress

A force tending to deform a body, expressed as force per unit area.

• There are forces acting normal and tangential to a surface.

Pressure is a type of stress that can act on a fluid at rest. pressure acts equally in all directions Tangential = shear stress The surface layer of frictional influence generates this shearing force and transmits it downwards as a flux of momentum.

Tangential stress acting on a grassy field

Stress in the Atmosphere

In the atmosphere, three particular forms of stress are acting on an air parcel:

• Pressure
• Viscous shear stress
• Reynolds stress

Photo: A. Christen

Stress is the force tending to produce deformation in a body. It is measured as a force per unit area. Three types of stress appear frequently in studies of the atmosphere: pressure, Reynolds stress, and viscous shear stress.

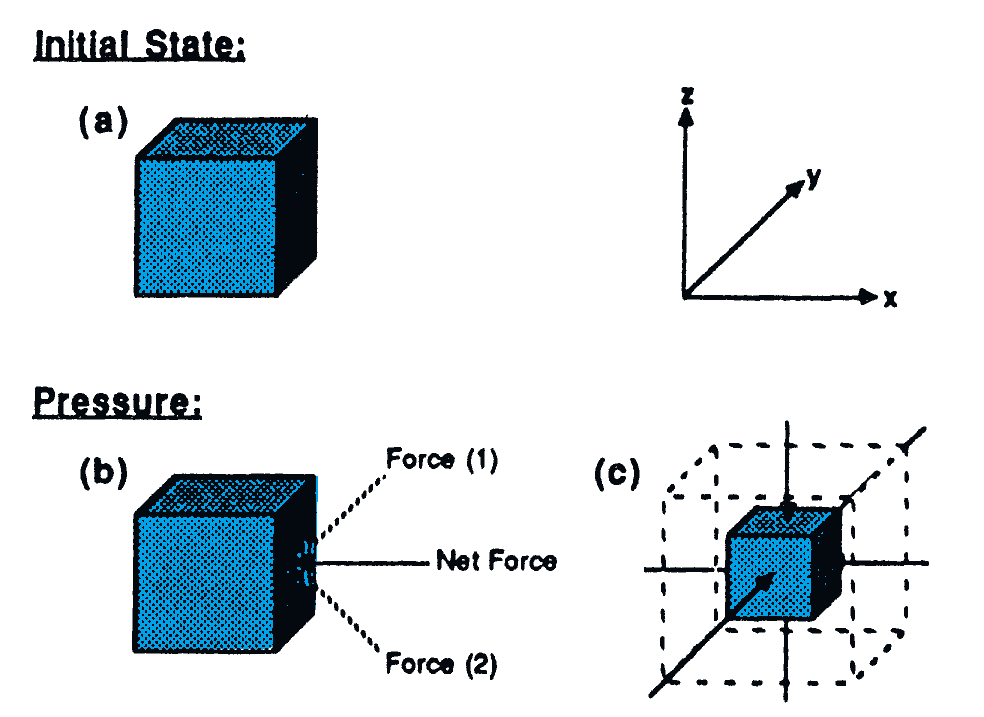
Pressure

• Pressure can act on an air parcel at rest.
• At a point, pressure acts isotropically and normal to the surface (normal force per unit area). Because it is not dependent on direction, pressure can be reduced to the scalar \(P\).
• Pressure changes always result in an isotropic compression or expansion of an air parcel.

R. B. Stull (1988): ‘An introduction to boundary layer meteorology’

Pressure is a type of stress that can act on a fluid at rest. For an infinitesimally small fluid element, such as idealized as the cube sketched in Fig 2.16a, pressure acts equally in all directions. Isotropic is the name given to characteristics that are the same in all directions (see Figs 2.4 and 2.5). If we consider just one face of this cube, as in Fig. 2.16b, we see that the isotropic nature of pressure tends to counteract itself in all directions except in a direction normal to (perpendicular to) the surface of the cube. Forces acting normal to all faces of the cube tend to compress or expand the cube, thereby deforming it (Fig 2.l6c). Because pressure is not dependent on direction, we need just one number to describe it at any point in space and time. Thus, pressure is a scalar.

Total Shear Stress

Viscous shear stress is important whenever there are shearing forces in a moving fluid (laminar or turbulent).

• These shearing forces are opposed to the intermolecular forces. Viscous stress is a function of the velocity gradients and the dynamic viscosity.

Reynolds stress is only found in turbulent flows. It is a result of convective movement of momentum surplus and momentum deficit eddies within the fluid.

R. B. Stull (1988): ‘An introduction to boundary layer meteorology’

Viscous stress exists when there are shearing motions in the fluid. The motion can be laminar or turbulent. When one portion of a fluid moves, the intermolecular forces tend to drag adjacent fluid molecules in the same direction. The strength of these intermolecular forces depend on the nature of the fluid: molasses has stronger forces than water, which in turn has stronger forces than air. A measure of these forces is the viscosity. The result of this stress is a deformation of the fluid

Reynolds stress exists only when the fluid is in turbulent motion. A turbulent eddy can mix air of different wind speeds into our cube of interest (Fig 2.l6d). When this different-speed air is incorporated into one face of the cube and not the opposite face, the cube deforms because of the velocity differences between those two faces

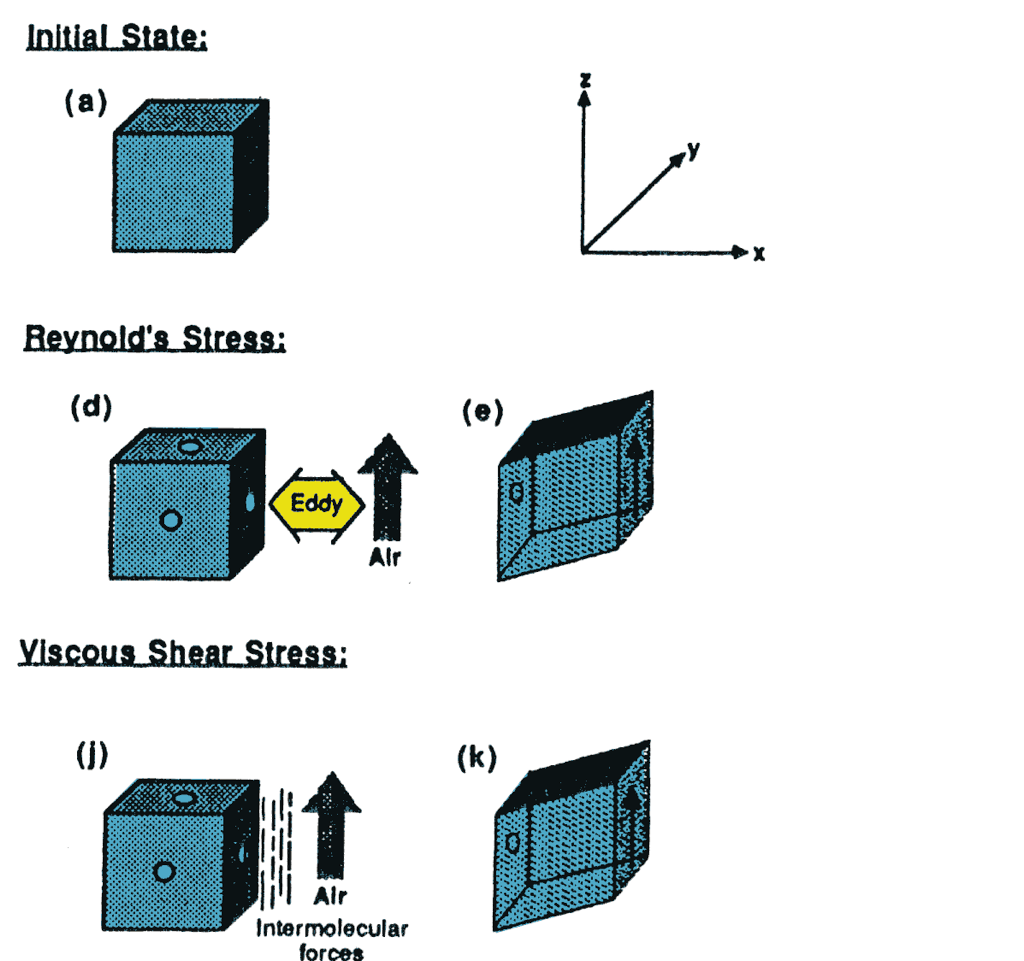
Reynolds stress

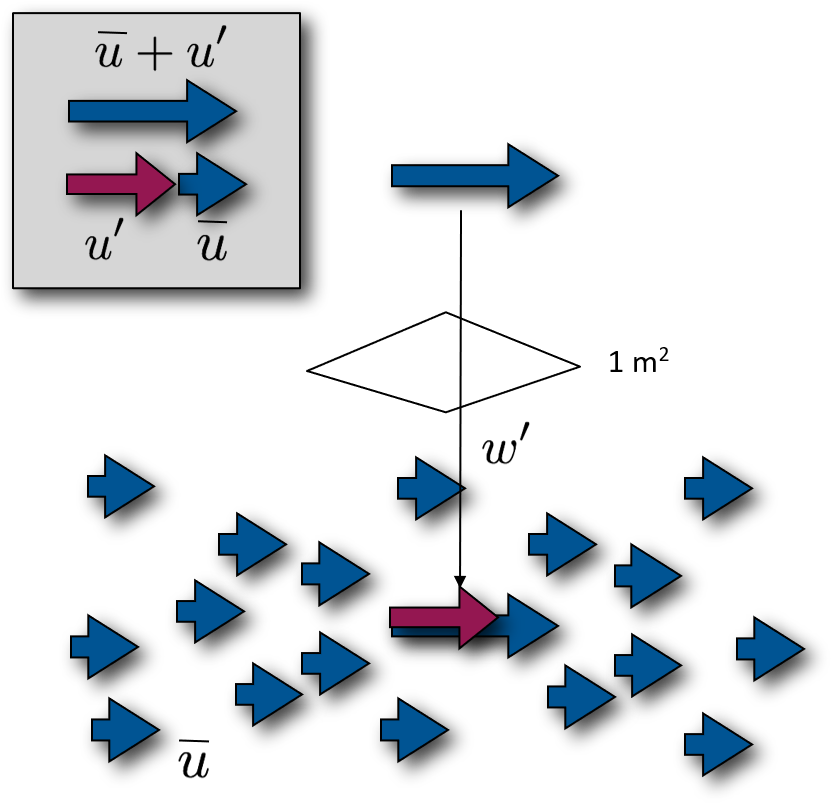
The flux of momentum is accomplished through random motion. Discrete ‘lumps’ (eddies) of the fluid are displaced by turbulence over a distance and there merge with the flow. Consequently eddies transport their momentum surplus or their momentum deficit (${u}) across a distance.

Simulation: O. Coceal, Univ. of Reading

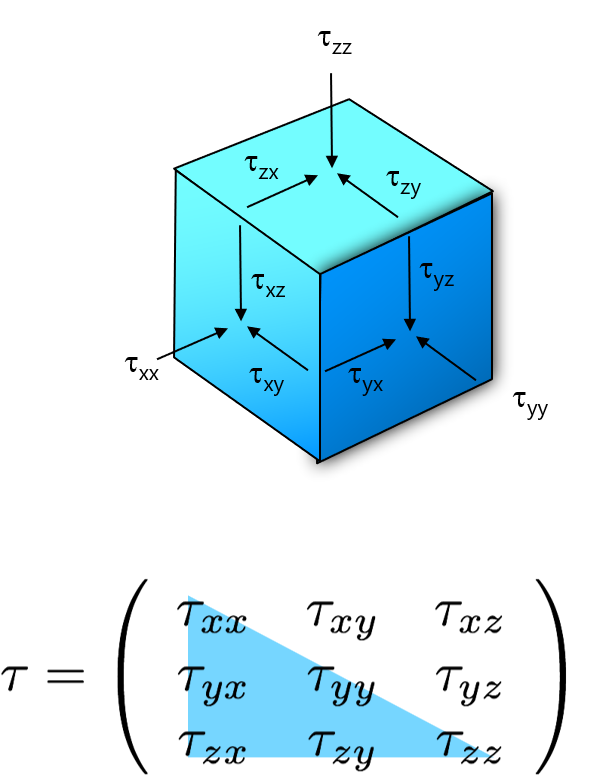
Stress Tensor

In a three dimensional view, we can define a stress tensor \(\tau\) that deforms a body

• It incorporates 9 stress vectors acting on one point in space.
  • The tensor is symmetric, so there are only 6 independent components (3 normal / 3 tangential).
  • A stress tensor can be separately written for the viscous shear stress and the Reynolds stress.

Delete?

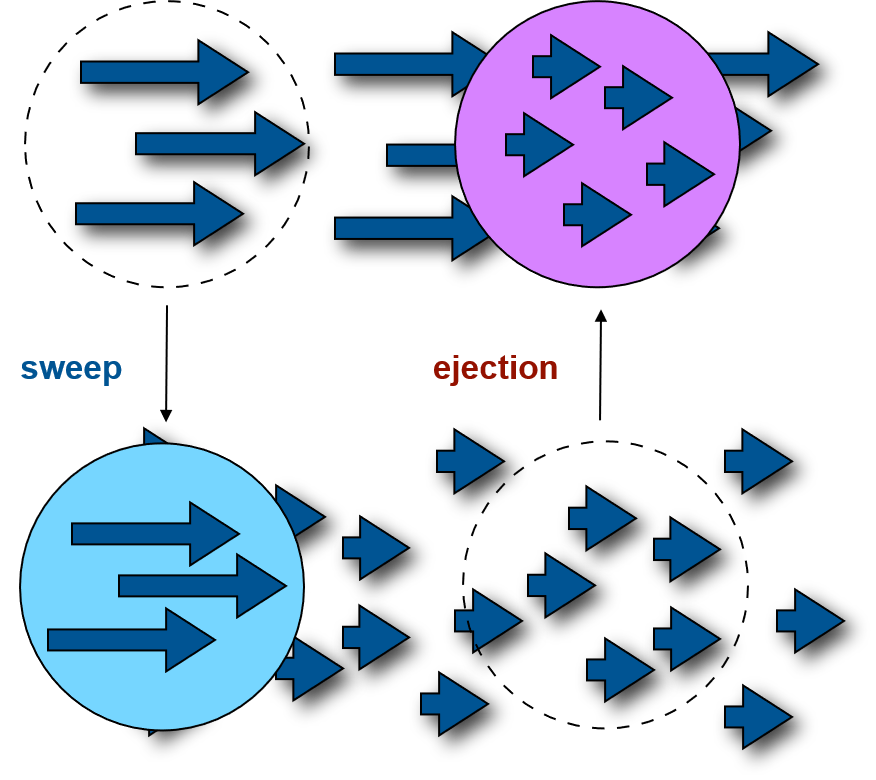
Sweeps and Ejections

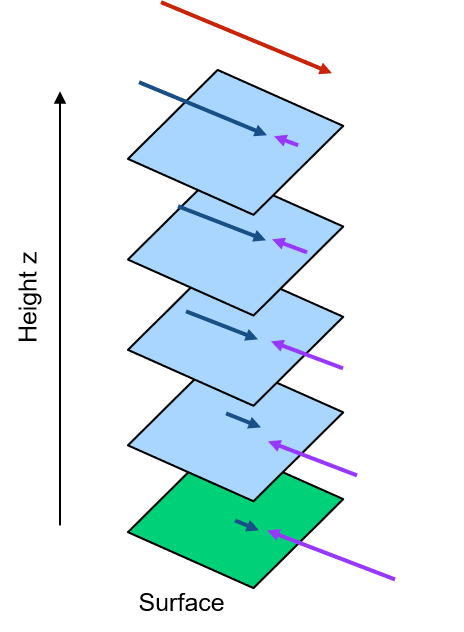
In the atmospheric boundary layer over flat terrain the transfer can be often simplified 1-dimensional (up/down only)

• Ejections Events transporting momentum deficit upward

• Sweeps Events transporting momentum surplus downward

Momentum Exchange

Joint probability density. Note the asymmetric PDF –By inspection, note that the larger probabilities occur as X and Y move in opposite directions. This indicates a negative covariance. Events transporting momentum deficit upward are called ejections. Events transporting momentum surplus downward are called sweeps. The surface layer of frictional influence generates this shearing force and transmits it downwards as a flux of momentum.

Work on handout

Mixing Length

The characteristic height for mixing to occur is the mixing length \(l\) and is likely related to the mean size of eddies.

Assume an eddy at level (\(z+l\)) with mean velocity \(\bar{u}_{(z+l)}\) moves down to \(z\) where mean velocity \(\bar{u}_{(z)}\) is less, by \(u^{\prime}\):

\[ u^{\prime} = \bar{u}_{(z+l)}-\bar{u}_{(z)} \]

so: \[ u^{\prime} = l\small\frac{\delta u}{\delta z} \qquad(1)\]

• i.e. extra velocity = increment in height x rate of change of velocity with height.

Mixing length is related to mean size of eddies. The characteristic height difference for mixing to occur is the mixing length l

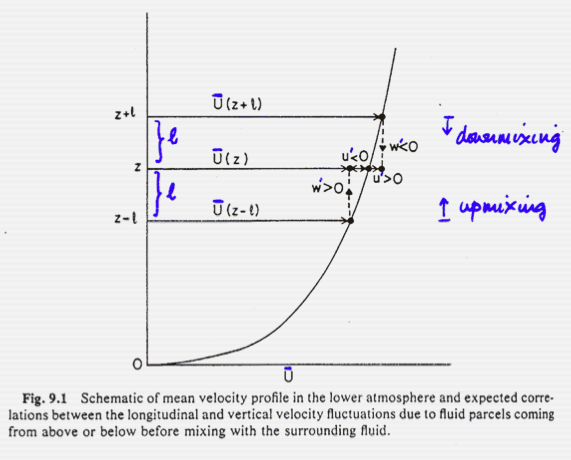
Reynolds stress and covariance

Assuming horizontal homogeneity, if an eddy merges to a new layer:

• It imports /subtracts \(\rho u^{\prime}\) amount of horizontal momentum per unit volume from/to the flow at level \(z\).

If the vertical velocity of the eddy is w’ then the instantaneous Reynolds stress (momentum flux) is

\[ \tau = -\rho u^{\prime} w^{\prime} \]

and in the time average

\[ \tau = -\rho \overline{u^{\prime} w^{\prime}} \]

Thus, stress and momentum flux are physically the same in a fluid such as air.

Friction Velocity

Assuming horizontal homogeneity: In turbulent shear flows, the Reynolds stress (momentum flux) is found to be proportional to the square of the mean flow velocity, which leads to the definition of the friction velocity \(u_*\) (units: m s-1)

\[ u_*^2 = \small\frac{\tau_0}{\rho} \qquad(2)\]

• Close to the surface, we can assume \(\tau = \tau_0\) and write: \(\tau = \rho u_*^2\)

• And because \(\tau = -\rho \overline{u^{\prime}w^{\prime}}\):

• A reasonable estimate of the friction velocity can be made from measurements of the Reynolds stress \(\overline{u^{\prime}w^{\prime}}\) close to the surface, i.e.

\[ u_* = \sqrt{-\overline{u^{\prime}w^{\prime}}} \qquad(3)\]

Shear Velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. Shear velocity is used to describe shear-related motion in moving fluids. It is used to describe:

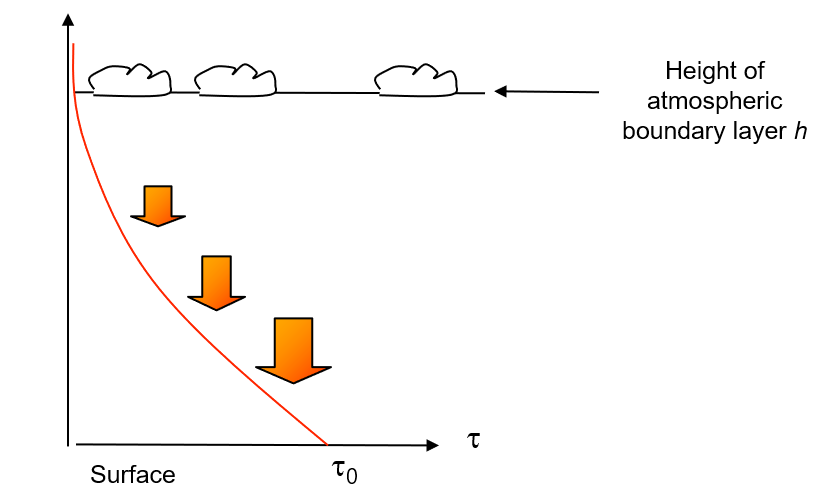
Vertical flux profile

The force is generated within the lowest layers and transmitted as a vertical flux of horizontal momentum mainly in terms of a Reynolds stress.

Take home points

• There are tangential and normal stresses that deform an air parcel in the atmosphere.
• Sweeps and ejections refer to part of eddies in a turbulent flow that move momentum up and down.
• Momentum transfer can be quantified using the covariance u’w’ and friction velocity u* is a global parameter that describes its square root in the lowest surface layer.