Dissipation of Turbulence

Learning Objectives

• Explain why there isn’t more and more turbulence in the atmosphere if there’s a continual supply of kinetic / thermal energy.
• Describe if there are limits to the scales of turbulent eddies in a system.
• Understand how we graph the size and duration of eddies.

Turbulent eddies in Jupiter are as large as the entire planet Earth (NASA)

Turbulence Generation (iClicker)

This type of turbulence is likely to occur on a calm sunny day with minimal winds:

• A: Thermally induced turbulence
• B: Mechanically induced turbulence
• C: Both of the above types are equally likely
• D: Neither, turbulence cannot occur without kinetic energy from wind to initiate it

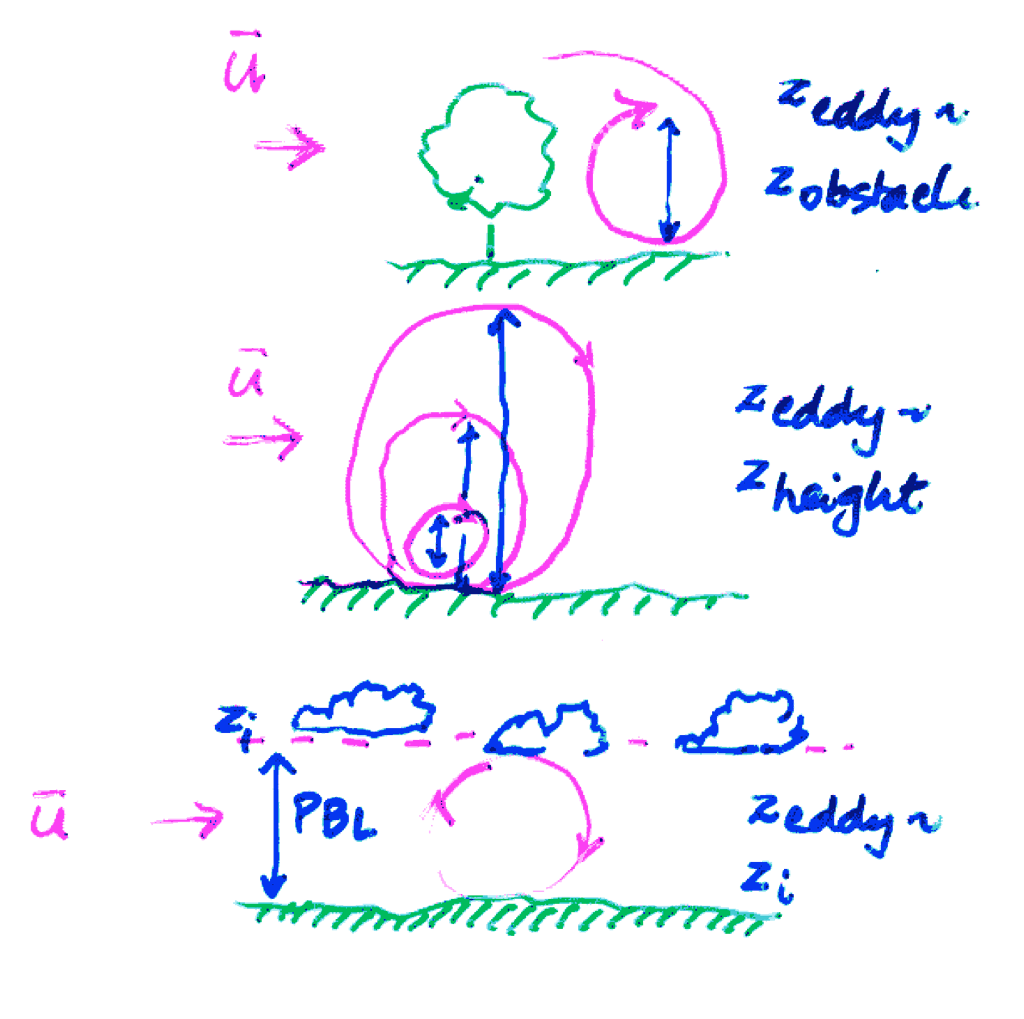
Scales of Eddies on Earth

it is believed that a turbulent flow consists of a hierarchy of eddies of a wide range of sizes (length scales). The range of eddy sizes increases with the Reynolds number of the overall mean flow. In particular, for the ABL, the typical range of eddy sizes is 10^-3 to 10^3 m. Turbulence can be considered to consist of eddies of different sizes. The region occupied by a larger eddy can also contain smaller eddies. Eddies of size l have a characteristic velocity u(l) and timescale t(l)  l/u(l).

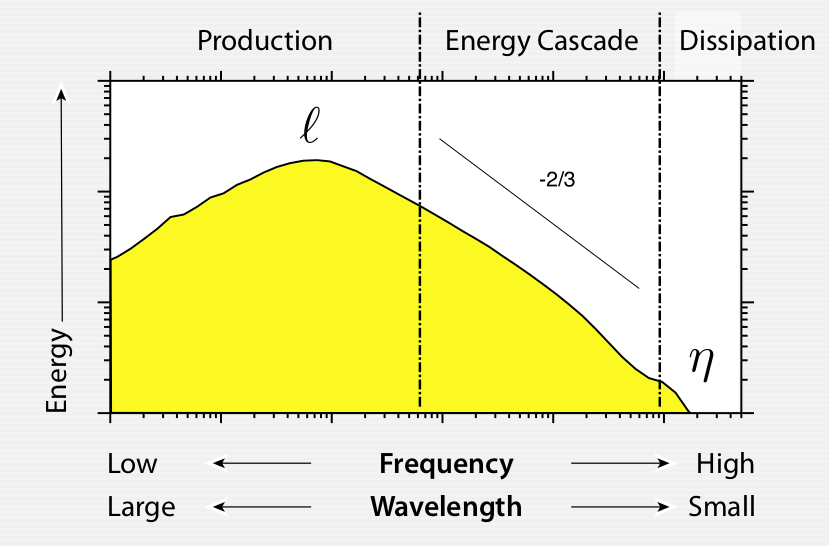
Energy Cascade Theory

Breakdown continues all the way down the inertial subrange to the molecular scale where eddies dissipate into heat. This is called the energy cascade.

The largest eddies are produced by mechanical or thermal convection (mean flow shear and thermal convection). These large eddies become dynamically unstable and produce eddies of somewhat smaller size, which themselves become unstable and produce eddies of still smaller size, and so on further down the scale. This cascade process is terminated when the Reynolds number based on the smallest eddy scales becomes small enough (order of one) for the smallest eddies to become stable under the influence of viscosity. At the smallest eddy sizes, the cascade of energy is dissipated into heat by molecular viscosity. The largest scale eddies have lengths on the order of a kilometer or three. These eddies are of the scale of the depth of the planetary boundary layer, which is approximately the height of the base of fair weather convective clouds. These large eddies are responsible for transport of mass and energy. Of the wide and continuous range of scales in a turbulent flow, a few have special significance and are used to characterize the flow itself. L = integral length scale. Size of the largest eddies in the flow – the size of the largest eddies in the flow account for most of the transport of momentum and energy. The integral length scale, l, is a measure of the largest eddy size in turbulent flow or the eddies receiving the most energy from the mean flow.

Separation between the largest and smallest length scales increases as the Reynolds number is increased.

Integral length scales

The integral length scale \(l\) of a turbulent flow depends on the processes that create it; \(l\) is a measure of the largest eddy size in the flow.

For mechanical turbulence this is the size of the obstacle, but

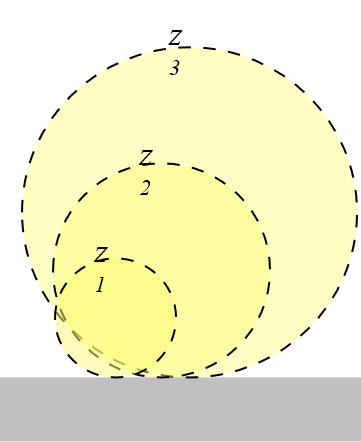
• Limit 1: height above ground

• Limit 2: depth of the PBL

The integral length scale, l, is a measure of the largest eddy size in turbulent flow They characterize the energy-containing range of eddy length scales. As the integral length scale increases with height above ground due to less damping by the surface boundary What you can resolve depends on where you are. Measure at same length scale you’re trying to resolve . Larger eddies look like the mean wind to you

Kolmogorov Microscale

The Kolmogorov microscale (\(\eta\)) depends on the fluid’s viscosity \(\upsilon\), and the rate of energy dissipation to heat (\(\epsilon\)):

\[ \eta = \upsilon^{\small\frac{3}{4}}\epsilon^{\small\frac{-1}{4}} \]{eq-Kolmogorov-Microscale}

In steady-state turbulence as often encountered in the ABL, the rate at which the energy is dissipated is exactly equal to the rate at which energy is supplied (by thermal and mechanical convection).

Another is the characteristic small-eddy scale or microscale of turbulence, which represents the length (eta) or time scale of most dissipating eddies The smallest length scales existing in a turbulent flow are those where the kinetic energy is dissipated into heat. For a statistically steady turbulent flow, the energy dissipated at the small scales, must equal the energy supplied at the large scales.

The dissipation rate per unit mass (e).

The Kolmogorov length scale is the smallest hydrodynamic scale in turbulent flows

Separating Scales - Fourier Transform

Scales of a turbulent flow are given by calculating a velocity spectrum:

Fourier transform: Decompose frequencies contributing to a time series

The turbulence spectrum is analogous to the spectrum of colours in a rainbow. White light consists of many colours (i.e. many wavelengths or frequencies) superimposed on one another. Raindrops act like a prism that separates the colours. We could measure the intensity of each colour to learn the magnitude of its contribution to the original light beam. We can perform a similar analysis on a turbulence signal using mathematical rather than physical devices (i.e. a prism) to learn about the contribution of each different eddy size to the total turbulence kinetic energy.

https://sknox01.github.io/GEOS300/applets/fouriertransform/

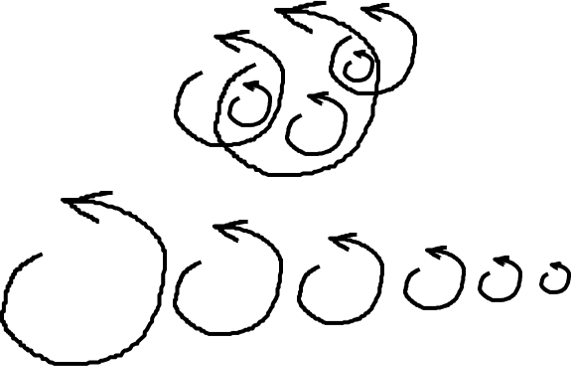
Spectra

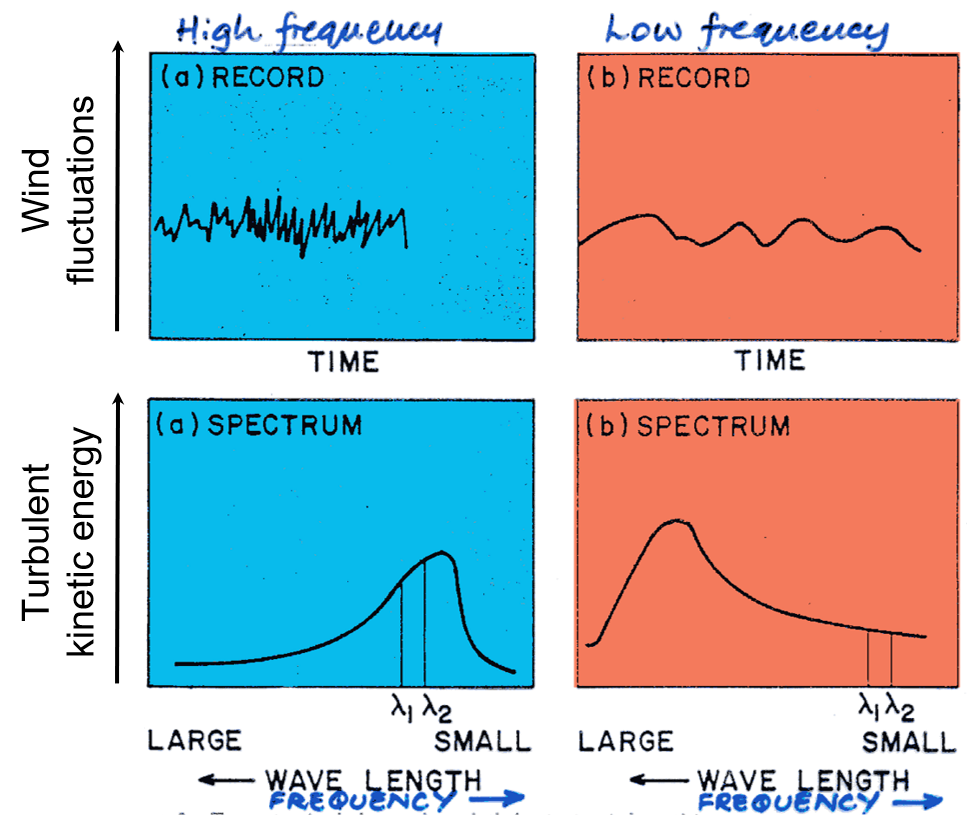
Size of eddies can be viewed as wavelength (\(\lambda\)) or as frequency (\(v\)).

• A turbulence spectrum shows the energy as function of \(\lambda\) or \(v\), i.e. it sorts a time series by eddy duration.

In white noise all waves in all frequencies show the same energy content

red noise is strong in longer wavelengths, similar to the red end of the visible spectrum. Spectral energy

Phenomena vs. Frequency

Example of the spectrum of wind speed measured near the ground. Small eddies have shorter time periods than large eddies. Peaks in the spectrum show which size eddies contribute the most to the TKE. The leftmost peak (100 h) corresponds to wind speed variations associated with the passage of fronts and weather systems. The next peak (24 h) shows the diurnal increase of wind speed during the day and decrease at night. The rightmost peak indicates the microscale eddies (10 s to 10 min). Within the rightmost peak we see that the largest eddies are usually the most intense. The smaller, high frequency, eddies are very weak, as previously discussed. Large-eddy motions can create eddy-size wind-shear regions, which can generate smaller eddies. Such a net transfer of turbulence energy from the larger to the smaller eddies is known as the energy cascade. There appears to be a distinct lack of wind-speed variation having time periods of about 30 min to 1 h. The lack of variation at the internediate time or space scales has been called the spectral gap. Motions to the left of the gap are said to be associated with the mean flow. Motions to the right constitute turbulence. The center of the gap is near the one-hour time period.

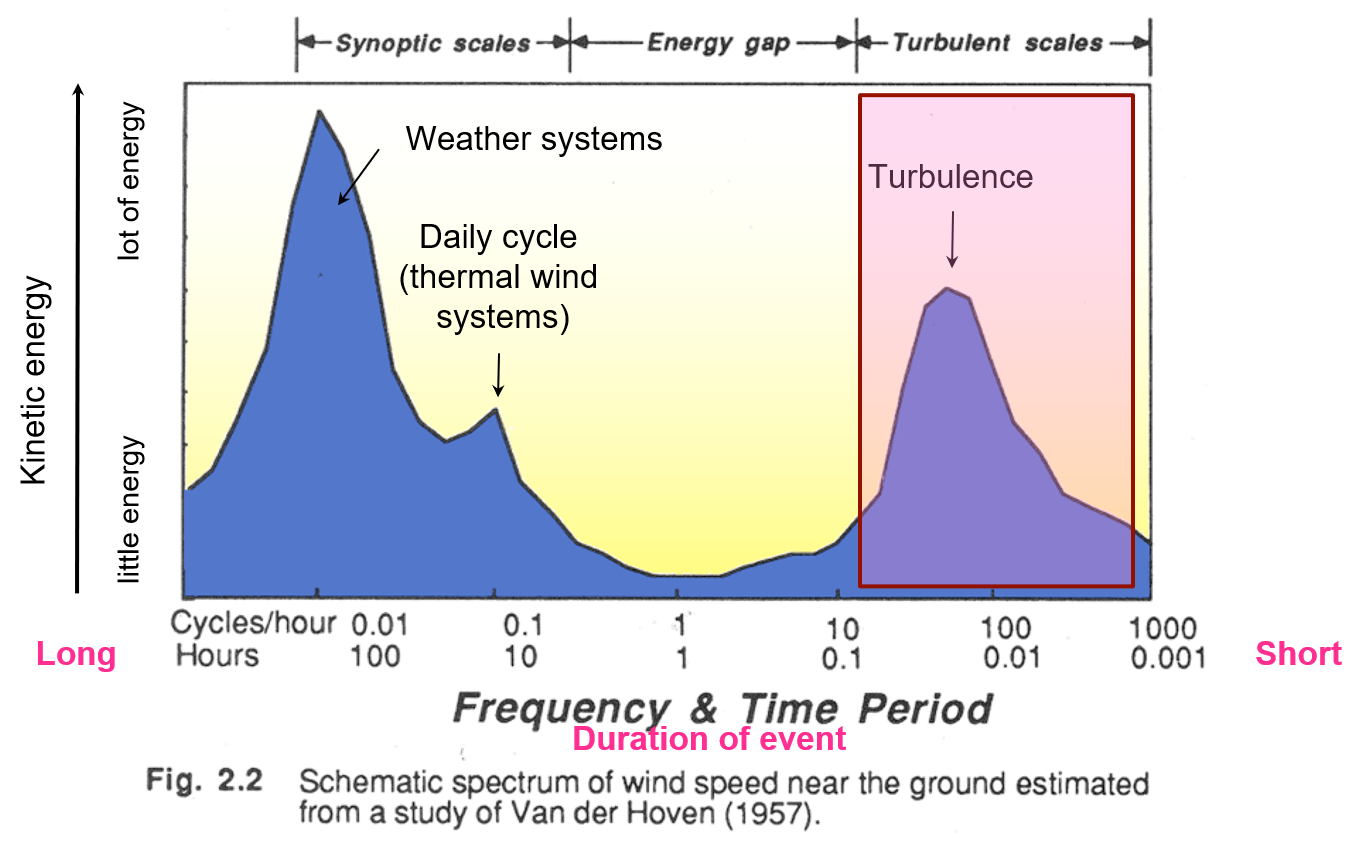
A spectrum of atmospheric turbulence

Three subranges, the production (energy containing) range, the energy cascade (inertial subrange) and the dissipation range. The turbulence in the energy production is produced by mechanical and thermal convection. The integral length scale, l, is a measure of the largest eddy size in turbulent flow or the eddies receiving the most energy from the mean flow.
In the energy cascade subrange, energy is neither produced or destroyed. Instead energy cascades from larger to smaller scales. The slope of the spectrum in the inertial subrange has a slope of –5/3 (or –2/3 when normalized by n). Such a net transfer of turbulence energy from the larger to the smaller scales is known as the energy cascade. At the smallest eddy sizes, the cascade of energy is dissipated into heat by molecular viscosity.

Inertial subrange: the spectra in this range also conforms to local isotropy. Correlations between velocity components are nil and there is no net transfer of turbulence in this subrange. The large-scale motions or eddies that receive energy directly from mean flow shear or buoyancy are expected to be inhomogeneous. But the small eddies, that are formed after many successive breakdowns of large and intermediate size eddies, are likely to become homogeneous and isotropic.

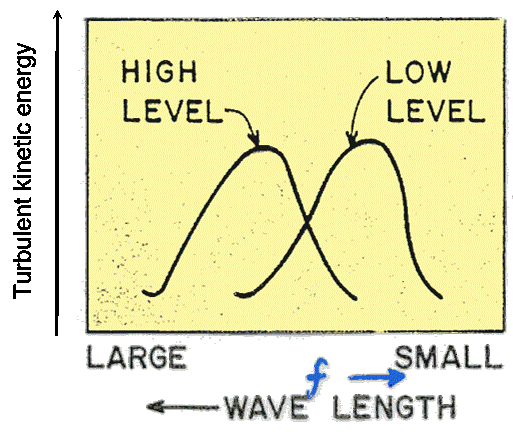
Schematic set of spectra

Influence of Height Above Ground

The integral length scale increases with height above ground due to less damping by the surface boundary

So the spectra move to the left, i.e., longer wavelengths become more dominant

As the integral length scale increases with height above ground due to less damping by the surface boundary, so do spectra move to the left.

Influence of Stability (iClicker)

For a review of stability, see here

Thermal convection will always continue once induced under which type of atmospheric conditions:

• A: Stable
• B: Neutral
• C: Conditionally Unstable
• D: Unstable

Influence of Stability

Turbulent fluctuations are:

• High frequency (seconds) in stable and neutral ABL, when only mechanical convection is present
• Low frequency (minutes) in unstable air when thermal convection is dominant

Directionality of turbulent motions

Isotropic Turbulence: The velocity fluctuations are independent of the axis of reference, i.e. invariant to axis rotation and reflection. Isotropic turbulence is by its definition always homogeneous . In such a situation, the gradient of the mean velocity does not exist, the mean velocity is either zero or constant throughout. Isotropic Turbulence: The statistical features have no directional preference and perfect disorder persists. Isotropic is the name given to characteristics that are the same in all directions

e = kinetic energy of the instantaneous deviations per unit mass

Isotropic turbulence is an idealized turbulent state in which the turbulent fluctuations are statistically uniform in all directions.

Homogeneous Turbulence: Turbulence has the same structure quantitatively in all parts of the flow field. Isotropic Turbulence: The statistical features have no directional preference and perfect disorder persists. Anisotropic Turbulence: The statistical features have directional preference and the mean velocity has a gradient.

Homogeneous Turbulence : The term homogeneous turbulence implies that the velocity fluctuations in the system are random but the average turbulent characteristics are independent of the position in the fluid, i.e., invariant to axis translation.

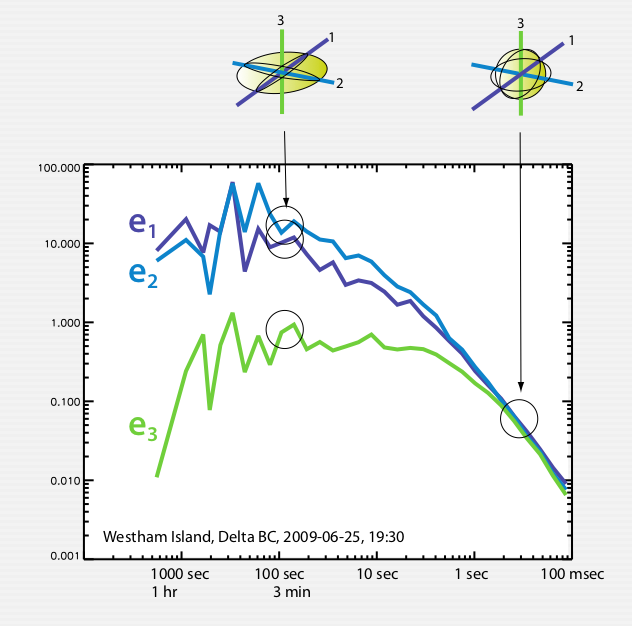
Kolmogorov’s theory of local isotropy

Initial eddies, created at the length scale \(l\) are likely directional:

• After many break-downs into smaller ones they have the tendency to return to isotopy.
  • Energy contained in one axis is transferred into other axes.

The large-scale motions or eddies that receive energy directly from mean flow shear or buoyancy are expected to be inhomogeneous (i.e. have turbulent energy that isn’t equal in all directions). But the small eddies, that are formed after many successive breakdowns of large and intermediate size eddies, are likely to become homogeneous and isotropic. Atmospheric turbulence is not homogeneous and isotropic when one con- siders its large-scale structure. The presence of mean wind shears and thermal stratification, at least in the vertical direction, are responsible for the generation and maintenance of turbulence. Horizontal inhomogeneities of mean flow and turbulence are often caused by variations of surface roughness, temperature, and topography. Isotropic Turbulence: statistical features have no directional preference – the system tries to reduce gradients

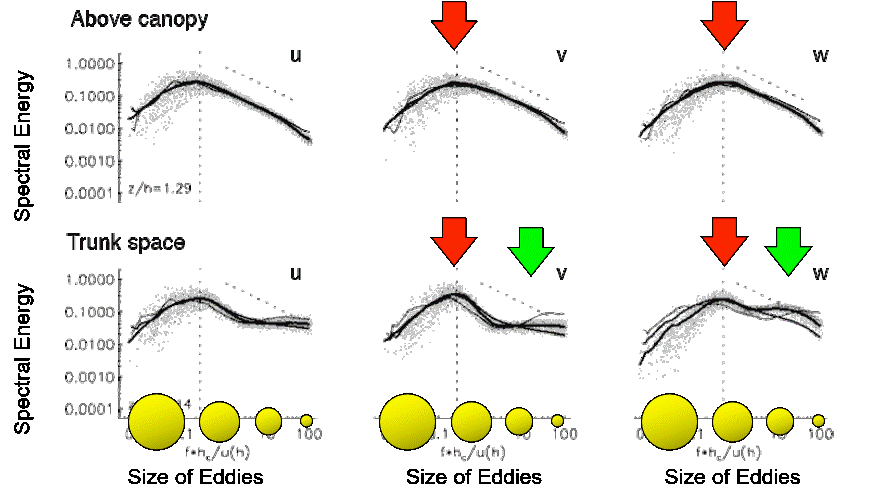
Turbulence spectra in plant canopies

In a fine structured canopy we observe a direct bypass from large eddies to small eddies without intermediate eddy sizes in the cascade.

• Large eddies are efficiently ‘cut’ into smaller ones by leaves, branches, stems - a process called wake and waving production.
• We call this process the spectral shortcut.

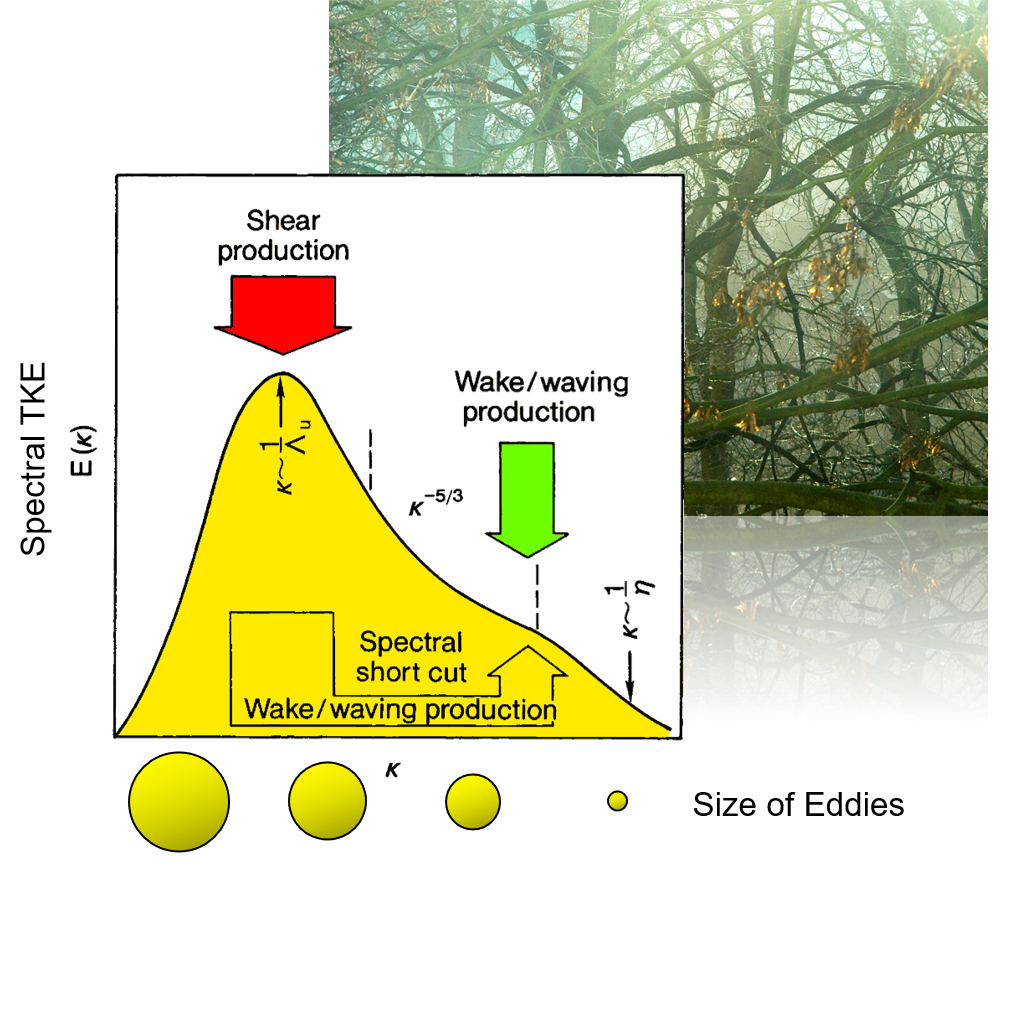
Spectral Shortcut of Turbulence in a Forest Canopy

Three subranges, the production range, the energy cascade and the dissipation range we observe a direct bypass from large eddies to small eddies without intermediate eddy sizes in the cascade. Large eddies are efficiently ‘cut’ into smaller ones by leaves, branches, stems - a process called wake and waving production. Spectral shortcut.

Take Home Points

• Eddies produced mechanically and thermally at larger scales (integral length scale l) break into smaller and smaller ones creating a steady-state energy cascade of eddy sizes.
• The integral length scale l is controlled by the height above ground and turbulence production mechanisms.
• At small scales - the Kolmogorov microscale η - eddies become stable again and energy is eventually dissipated to heat.
• The size (duration) of eddies can be graphed using an energy spectrum. A spectrum sorts the energy contained in turbulence according to duration (or length) of eddies.

mechanical turbulence this is the size of the obstacle

Midterm (iClicker)

Your midterm is:

• Wednesday March 13th
• Open Book
• Asynchronous (submitted on canvas)
• Not timed, but must be completed within 24 hours
• All of the above

Midterm Review

Part 1 Written answers (45%)

• 1 Problem Question: multi-part, involving calculations

• Energy balance and heat conduction

2 Short answers questions

• Brief, but thorough responses
• Bullet point format fine where applicable

Part 2 Automated marking (55%)

• 2 calculation questions:
  • Radiation budgets and geometry
  • Partial credit offered for work (will require manual review, wont be adjusted immediately)
• 6 or 7 multiple choice
• 2 or 3 fill in the blank
• 1 matching question