Longwave Radiation

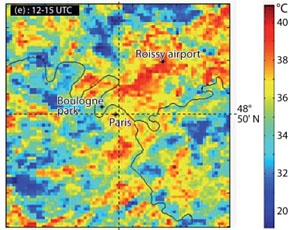
Peak emissions band of the Earth-Climate System

Learning Objectives

• See how radiation laws apply to long-wave radiative exchange and how long-wave radiation can interact with surfaces.

• Explain how we can calculate longwave outgoing radiation, and how it relates to surface emissivity.
• Know how we can estimate / model longwave incoming radiation and the emissivity of the atmosphere.

People in front of a heated building in winter as seen in the thermal infrared by a thermal camera (Source: A. Christen)

What is ‘Longwave’ radiation?

Short-wave (VIS) D. Scherer, Ecology Department, TU Berlin

Longwave (TIR) D. Scherer, Ecology Department, TU Berlin

Measuring Long-wave Radiation

Numerous instruments can measure long-wave radiation received in a particular field of view (FOV), within a particular band, and/or with a particular spatial resolution.

Thermal camera

Pyrgeometer

Thermal satellite channel

A radiometer measures the long-wave radiance received in a particular field of view (FOV), within a particular band, and with a particular spatial resolution. In remote sensing, sensors are built to pick up those specific spectral bands. Near IR, Mid-IR, Far IR Demo here

Stefan-Boltzmann Law: Grey Body

Natural objects (called grey bodies) are not full radiators. Their emittance is given by adapting the Stefan-Boltzman law:

\[ E_g = \epsilon\sigma_b T^4 \qquad(1)\]

where \(\sigma = 5.67 * 10^-8\)

• where \(\epsilon\) is their surface emissivity. Emissivity is the ratio of the actual emission to that of a blackbody (i.e. \(\epsilon\) = 1.0).
• This law is the basis of remote sensing in the TIR

Table 1: Long-wave emissivity coeficients (\(\epsilon_{LW}\)) for selected surfaces

Surface	Long wave Emissivity epsilon_ LW
Soil	0.90 – 0.98
Grass	0.90 – 0.95
Crops	0.90 – 0.99
Forests	0.97 – 0.99
Water	0.92 – 0.97
Iron	0.13 – 0.28

All bodies possessing energy (i.e. whose temperatures are above absolute zero, 0 K = −273.2◦C) emit radiation. If a body at a given temperature emits the maximum possible amount of radiation per unit of its surface area in unit time then it is called a black body. Such a body has a surface emissivity ε equal to unity. If the body is not a full radiator. Emissivity = absorptivity (low emissivity = reflects much of the radiant thermal energy) The map shows the long-wave emittance and reflectance of the land and ocean surface  Stefan–Boltzmann constant (sigma)

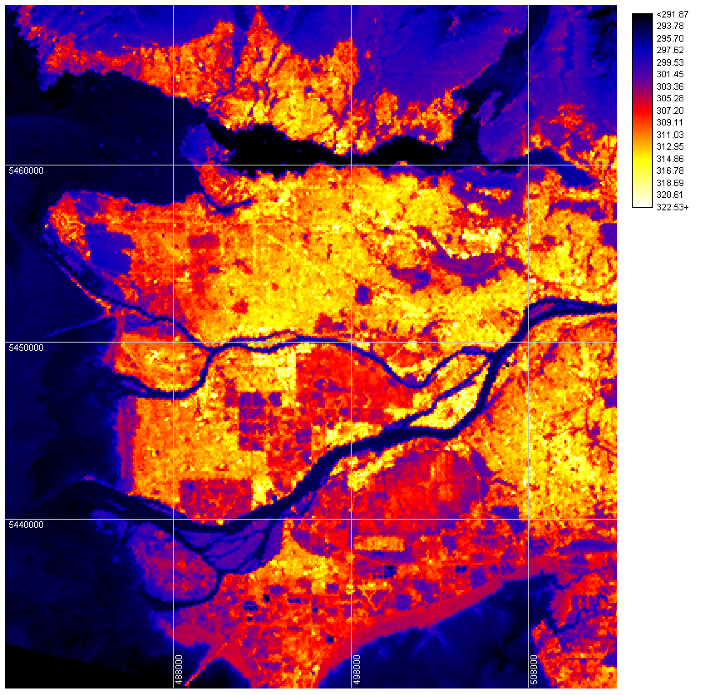
Emittance (W m^-2) of Vancouver seen from ASTER satellite Sept 3 2010 12:24 PDT

Advanced Spaceborne Thermal Emission and Reflection Radiometer on the Terra satellite launched into Earth orbit by NASA in 1999 The figure visualizes radiation measured between λ = 8μm and λ = 13μm by a satellite sensor The map shows the long-wave emittance and reflectance of the land and ocean surface

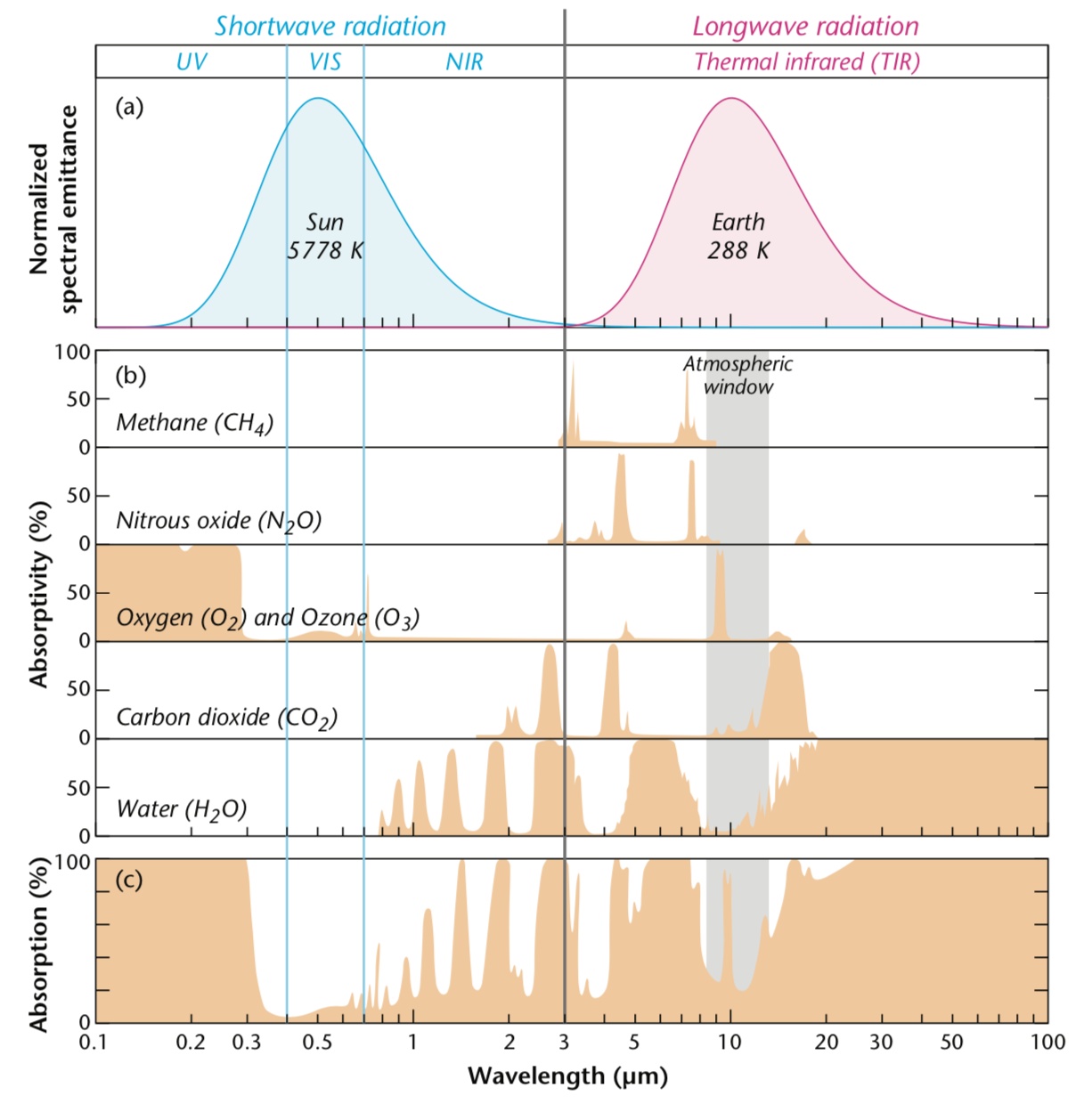
Atmospheric Window(s)

The satellite measures in this range because this is the atmospheric window in the long-wave part of the spectrum. In this range a cloudless atmosphere is quite transparent, as only a few trace gases absorb radiation. This allows us to see the surface, and not the intervening atmosphere.

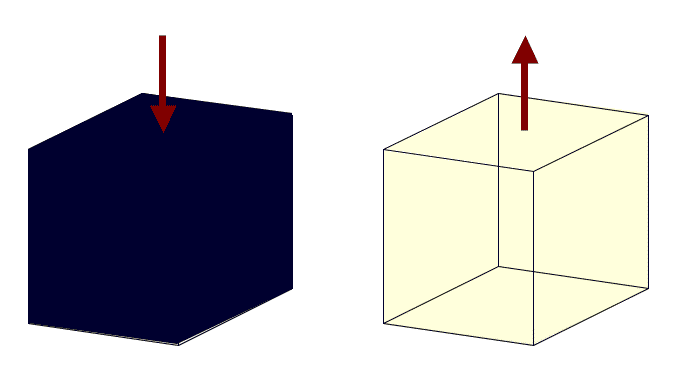
Kirchhoff’s law

\[ \zeta_{\lambda} = \epsilon_{\lambda} \qquad(2)\]

• Assuming no transmission the absorptivity of a body (\(\zeta_\lambda\)) equals its emissivity (\(\epsilon_\lambda\)) at a given wavelength.
  • A good absorber is a good emitter

For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.

Kirchhoff’s Law (iClicker)

Plants are good absorbers of \(SW\) radiation, so why don’t they emit just as much \(SW\) as they absorb?

• A: They aren’t hot enough (Stefan-Boltzmann)
• B: The do emit \(SW\), we call this Albedo

Kirchhoff’s Law

Kirchhoff’s law only applies if the wavelength considered is the same – do not mix them together.

• Kirchhoff’s law only has relevance to long-wave exchange in climatology.
  
• The law does not apply to fluorescent objects, which can absorb energy at a given a wavelength and release it at another one.

Mass-Radiation Interactions

\[ \zeta_\lambda + \Psi_\lambda + \alpha_\lambda = 1 \qquad(3)\]

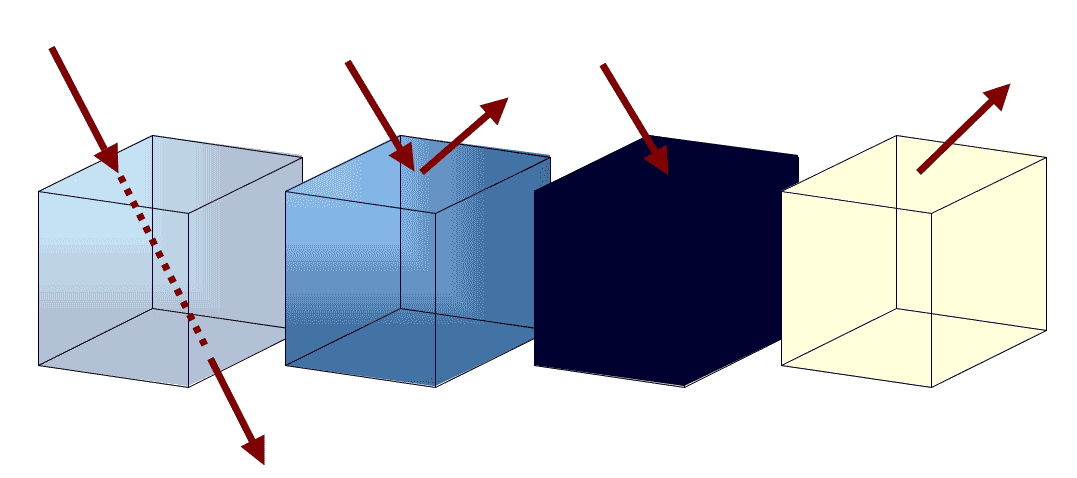
Transmission (\(\Psi_\lambda\)), Reflection (\(\alpha_\lambda\)), Absorption (\(\zeta_\lambda\)), Emission (\(\epsilon_\lambda\))

Long-wave Reflection

Most (solid) surfaces are opaque to long-wave (i.e., \(\Psi_{LW} \approx 0\)), so we can simplify our radiation conservation equation for \(LW\): \[ \zeta_{LW} + \alpha_{LW} = 1 \qquad(4)\]

\[ \alpha_{LW} = 1 - \epsilon_{LW} \qquad(5)\]

Long-wave Reflection (iClicker)

Which surface would you expect to have the highest \(\alpha_{LW}\)?

• A Peat (organic soil)
• B Wood
• C Steel (Iron-carbon alloy)
• D Wheat
• E A Cow

Table 2: Long-wave emissivity coeficients (\(\epsilon_{LW}\)) for selected surfaces

Surface	Long wave Emissivity epsilon_ LW
Soil	0.90 – 0.98
Grass	0.90 – 0.95
Crops	0.90 – 0.99
Forests	0.97 – 0.99
Water	0.92 – 0.97
Iron	0.13 – 0.28

Long-wave Reflection

Glass transmits a substantial fraction of visible light, but is relatively opaque to \(LW\)

Low-E, or low-emissivity, glass was created to minimize the amount of infrared and ultraviolet light that comes through your glass, without minimizing the amount of light that enters your home. Low-E glass windows have a microscopically thin coating that is transparent and reflects heat.

Net Long-wave Flux Density

The net long-wave radiation flux density (\(LW^*\)) at the surface is the difference between the input from the atmosphere above (\(LW\downarrow\)) and the output surface (\(LW\uparrow\)).

\[ LW^* = LW\downarrow - LW\uparrow \qquad(6)\]

• Surface output includes both emissions from surface and reflected \(LW\downarrow\)
  • Differs from \(SW*= SW\downarrow - SW\uparrow\)
  • \(SW\uparrow\) is only reflected \(SW\), earth doesn’t emit \(SW\)!

Long-Long-wave Flux Density

Net Long-wave Flux Density

We can re-formulate the previous equation in terms of the Stefan-Boltzmann Law:

\[ LW^* = LW\downarrow - \epsilon_{LW}\sigma_b T_s^4 -(1-\epsilon_{LW})LW\downarrow \qquad(7)\]

• How is this equivalent to Equation 6

• Stefan-Boltzman gives us emissions from a surface of temperature \(T_s\) with a long-wave emissivity of \(\epsilon_{LW}\)

• \((1-\epsilon_{LW})\) gives us reflectivity

Clouds, when present, are the major contributors to the incoming longwave radiation to the surface. They radiate like blackbodies (e ^ 1) at their respective cloud base temperatures. In passing through the atmosphere, a large part of the terrestrial radiation is absorbed by atmospheric gases, such as water vapor, carbon dioxide, nitrogen oxides, methane, and ozone. In particular, water vapor and CO2 are primarily responsible for absorbing the terrestrial radiation and reducing its escape to the space (the so-called greenhouse effect). The atmospheric gases and aerosols which absorb energy also radiate energy.

Estimating Surface Emissivity

We can compare the apparent surface temperature \(T_r\), which assumes the surface is a black body: \[ \sigma T_r^4 = \epsilon_{s} T_s^4 + (1-\epsilon_{s})LW_{\downarrow} \qquad(8)\]

In reality, we have both emission and reflection. We can re-arrange to isolate \(T_s\) \[ T_s = [\frac{\sigma T_r^4-(1-\epsilon_{s})LW_{\downarrow}}{\epsilon_{s}\sigma}] \qquad(9)\]

then substitute \(sigma T_k^4\) (\(T_k\) = apparent sky temperature) and re-arrange again: \[ \epsilon_{s} = \frac{T_r^4-T_k^4}{T_s^4-T_k^4} \qquad(10)\]

Infrared thermometer with emissivity = 1

Sky Temperature

\[ LW_\downarrow = \epsilon_{sky} \sigma T_{sky}^4 \qquad(11)\]

Apparent sky temperature is calculated by setting \(\epsilon{sky} = 1\) \[ LW_\downarrow = \sigma T_{k}^4 \qquad(12)\]

Calculating \(LW_\downarrow\)

• Screen level observations are typically available from regular climate stations for air temperature (\(T_a\)) and sometimes vapour pressure (\(P_v\)) but not \(LW_\downarrow\)
• If we are interested in estimating \(LW_\downarrow\) across full long-wave range (3 to 100 µm) we need a bulk value of \(\epsilon_a\) for both cloudless and cloudy cases.
• Several equations are available to estimate \(\epsilon_a\) from screen-level \(T_a\) and \(P_v\).

A standard Stevenson-screen sheltering sensors to measure air temperature and humidity (Photo: A. Christen)

Calculating \(LW_\downarrow\) - How to estimate \(\epsilon_a\)

• Using \(T_a\) and \(P_v\) to estimate \(\epsilon_a\) works because:
  • \(T_a\) and \(P_v\) are the main controls that change in the atmosphere
  • Variations in CO2, O3 and other greenhouse gases are small.
  • \(T_a\) and \(P_v\) are largest and show their greatest variation near the ground. Approximately 50% of \(LW_\downarrow\) originates from 0 to 100m.

Emissivity varies with temperature EQUATION FOR \(P_v\)

Calculating \(LW_\downarrow\) (Prata 1996)

\[ \epsilon_a = [1-(1+zeta)\exp{-(a+b\zeta)^{0.5}}] \qquad(13)\]

where a = 1.2, b=3.0, and \(\zeta = 46.5\frac{P_v}{T_a}\) with \(T_a\) in Kelvin and \(P_v\) in hPa.

where you can calculate \(P_v\) from RH as:

\[ RH=\frac{P_v}{P_v^*} \qquad(14)\]

and approximate \(P_v^*\) using the Tetens equation:

\[ P_v^* = 6.112\exp{17.62\frac{T_a}{243.12+T_a}} \qquad(15)\]

Note that \(T_a\) must be in \(C^\circ\) for this approximation. It will give \(P_v^*\) in hPa.

Td =  temperature at which the air can no longer “hold” all of the water vapor which is mixed with it, and some of the water vapor must condense into liquid water.  All such empirical equations are specific to the place where they were developed. Second, all such equations are daily averages that ignore the actual vertical temperature structure. Third, they assume perfectly clear skies, which may or may not be true. Fourth, one approach uses measurements with all their associated errors. Can get Sky emissivity from temperature and LWin

Calculating \(LW_\downarrow\) (iClicker)

At 15:00, February 2nd, \(T_a = 9 ^\circ\) and \(RH = 80%\), what was \(LW_\downarrow\)?

import numpy as np

class get_epsilon_a():
  def __init__(self,T_a,RH):
    if T_a < 100:
      self.T_a = T_a
      self.T_ak = T_a+273.15
    else:
      self.T_ak=T_a
      self.T_a=T_a-273.15
    if RH>1:
      self.RH=RH*.01
    else:
      self.RH=RH
    self.Prata()

  def Prata(self):
    self.Pv_from_RH()
    a = 1.2
    b = 3
    zeta = 46.5*(self.P_v/self.T_ak)
    self.epsilon_a = 1-(1+zeta)*np.exp(-(a+b*zeta)**0.5)

  def Pv_from_RH(self):
    P_v_star = 6.112*np.exp(17.62*self.T_a/(243.12+self.T_a))
    self.P_v = self.RH*P_v_star
e = get_epsilon_a(9,80)
e.epsilon_a

0.7709475025549156

• A 0.77
• B 0.88
• C 0.66
• D 0.55
• E 0.99

Effects of Temperature and Humidity (iClicker)

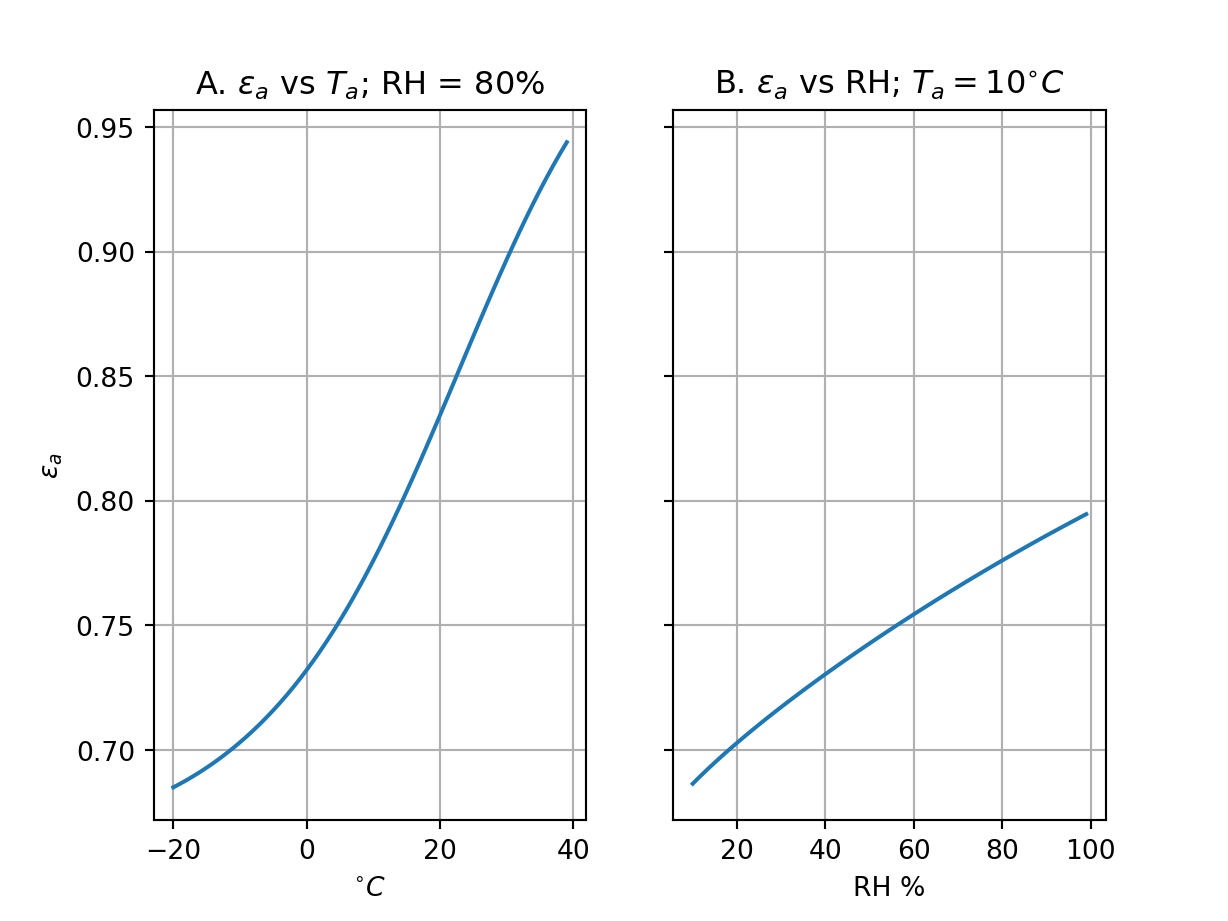
Which property has a stronger effect?

• A \(T_a\)
• B \(RH\)

UBC Energy Balance Station “Westham Island” (Photo: A. Christen)

Measures global and diffuse radiation

Diurnal Course - Clear vs Cloudy Sky

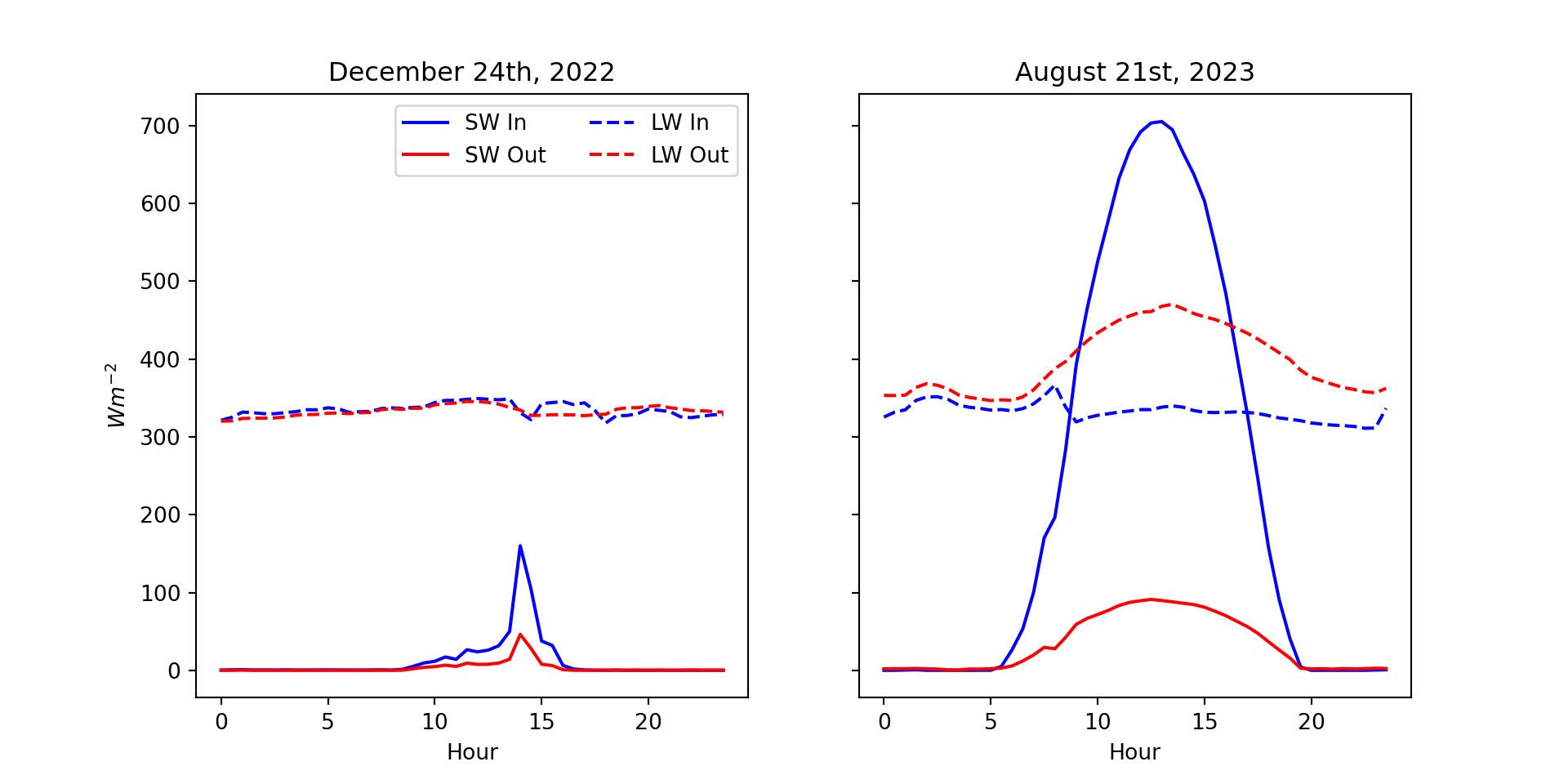
Effect of Clouds on Longwave Irradiance

With a clear-sky, \(LW_\downarrow\) originates from all layers of the atmosphere, because the atmosphere is partly transparent (‘atmospheric window’ open). With clouds \(LW_\downarrow\) originates from the cloud base and the atmosphere below the cloud, because the cloud is opaque to long wave (‘atmospheric window’ closed).

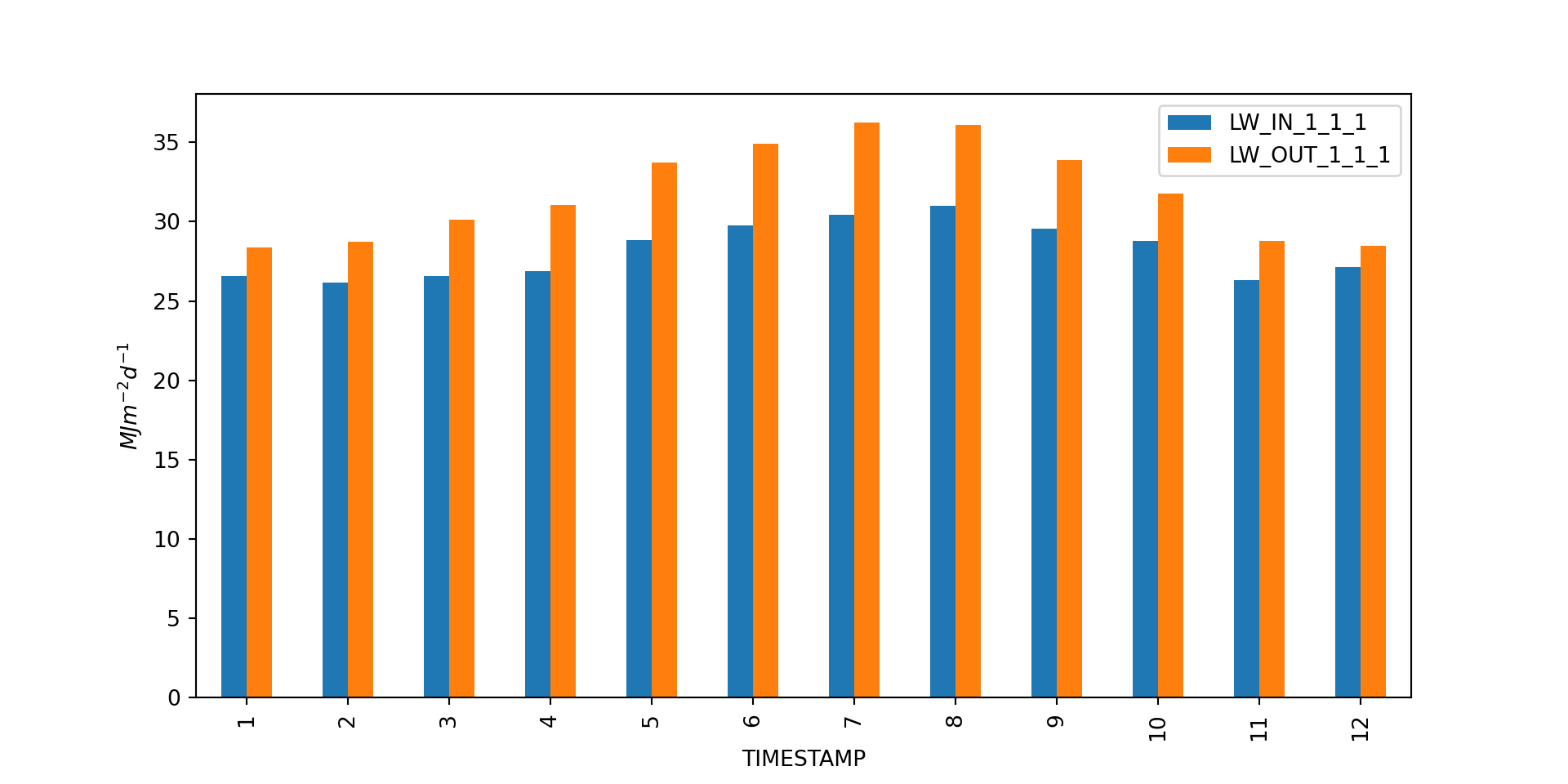
Monthly totals of \(LW_\downarrow\) & \(LW_\uparrow\) at CA-DBB

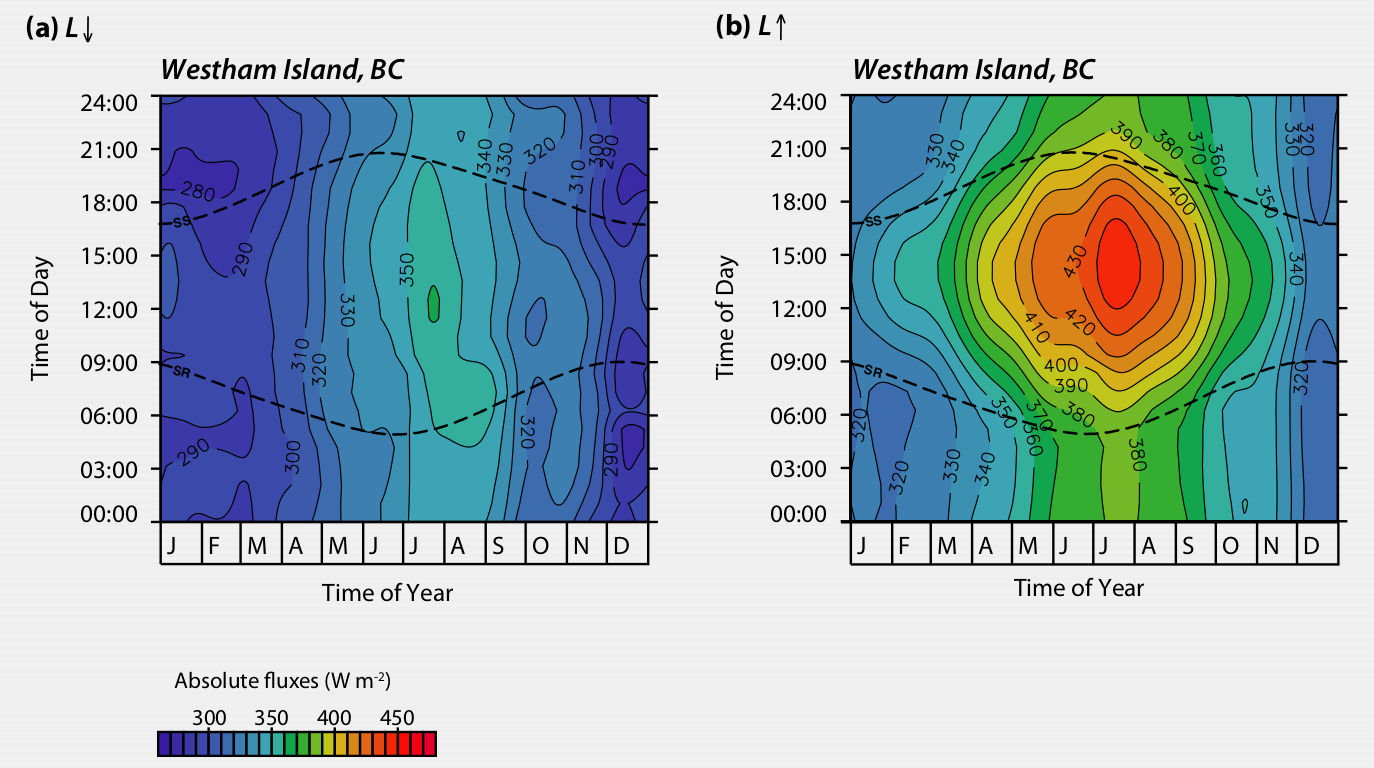
‘Fingerprint’ of \(LW_\downarrow\) and \(LW_\uparrow\) measured in Vancouver

Take Home Points

• Radiation laws apply the same way to the longwave part of the spectrum - but Kirchhoff’s law and the concept of emissivity become relevant.
• The net-long wave radiation is driven by the difference in apparent sky and surface temperatures and hence clouds and thermal surface properties are controlling radiative exchange in the long-wave.