Shortwave Radiation

Atmospheric Transmission & Surface Reflection

Today’s learning objectives

Describe how radiation interacts with mass.

• Understand how can we determine the transmission of short-wave radiation through the atmosphere.
• Describe how we can quantify and model the short-wave spectral properties of a surface.
• Explain how a surface’s reflectivity is affected by surface geometry.
• Understand how the sun’s position relative to an object affects reflectivity.

Mass-Radiation Interactions

\[ \zeta_\lambda + \Psi_\lambda + \alpha_\lambda = 1 \qquad(1)\]

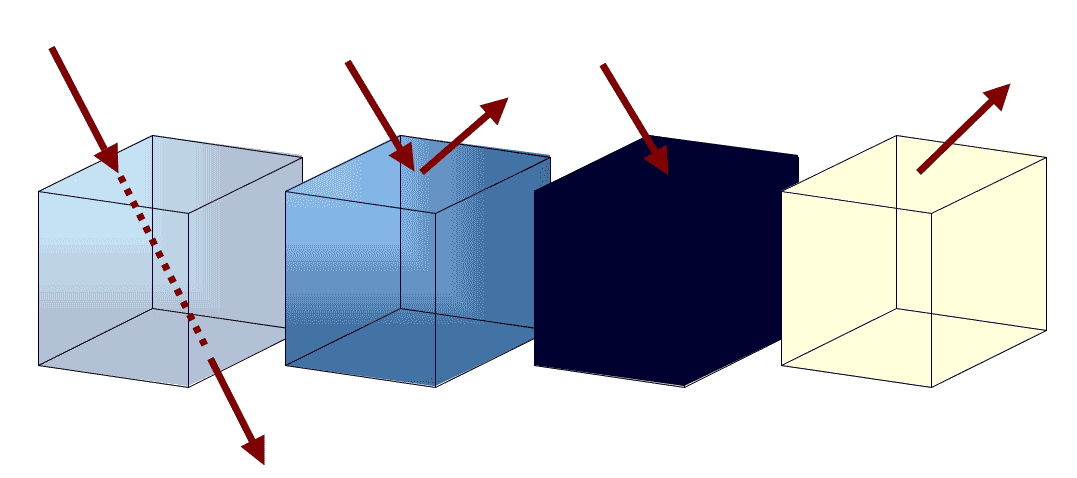
Transmission (\(\Psi_\lambda\)), Reflection (\(\alpha_\lambda\)), Absorption (\(\zeta_\lambda\)), Emission (\(\epsilon_\lambda\))

Radiation of wavelength λ incident upon an object must either be transmitted through it or be reflected from its surface, or be absorbed. This is a statement of the conservation of energy.

To calculate \(SW_\downarrow\) at Earth’s surface, we need to know the effect of the atmosphere in depleting solar radiation.

The Atmosphere depletes the solar beam as it passes through by an amount depending upon the length of its path, and the properties of the air. Gases, droplets and particles (especially ozone, water vapour, dust, clouds and smoke) have their own set of radiative properties with respect to the incident short-wave radiation, thus part of the beam is reflected (scattered), a part is absorbed and the rest is transmitted to the surface.

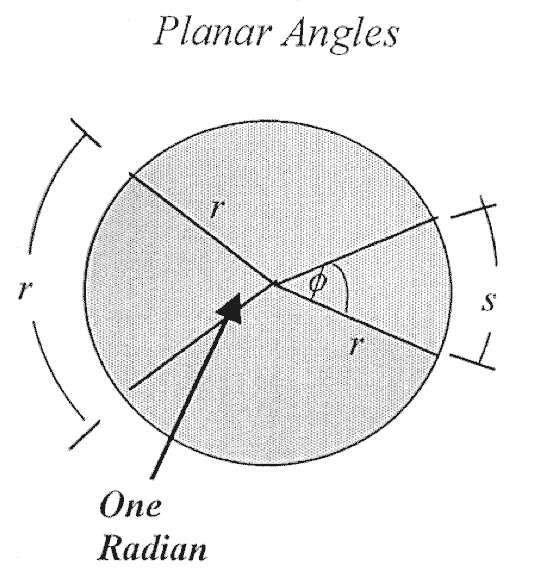
Planar angles

One radian (rad) is the angle which is subtended at the center of a circle of radius \(r\), by an arc of length \(r\).

• An arc of length \(s\) encloses an angle \(\phi = \frac{s}{r}\)
• The full circle (360\(^\circ\)) is \(2\pi r\)
  • 1 radian = 57.3 degree

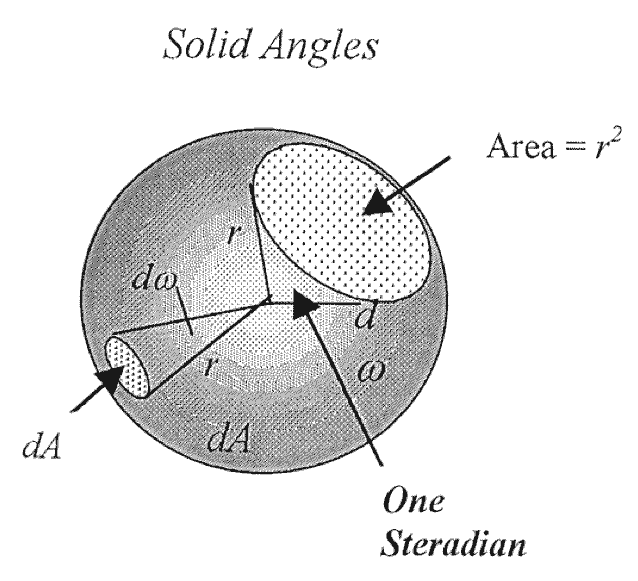
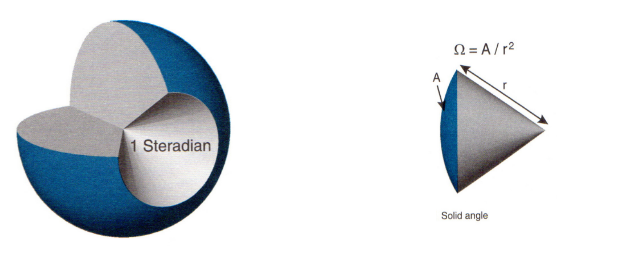
Solid angles

One steradian (sr) is the solid angle subtended at the center of a sphere of radius r by an area on the surface equal to r²

• An area \(dA\) encloses a solid angle \(d\omega = \frac{dA}{r^2}\)
  
• The full sphere = \(4/pi sr\)

A Steradian “cuts out” an area of a sphere equal to (radius)2.  Area of a small differential surface element A differential solid angle, indicated as dω (omega), delimits a cone in space So a sphere measures 4π steradians. Likewise a steradian is 1/12.57, or about 8% of a sphere.

 

Solid Angles

Definitions

Radiant intensity is the radiation flux per unit \(sr\) from a point source. The unit of radiant intensity is W sr^-1

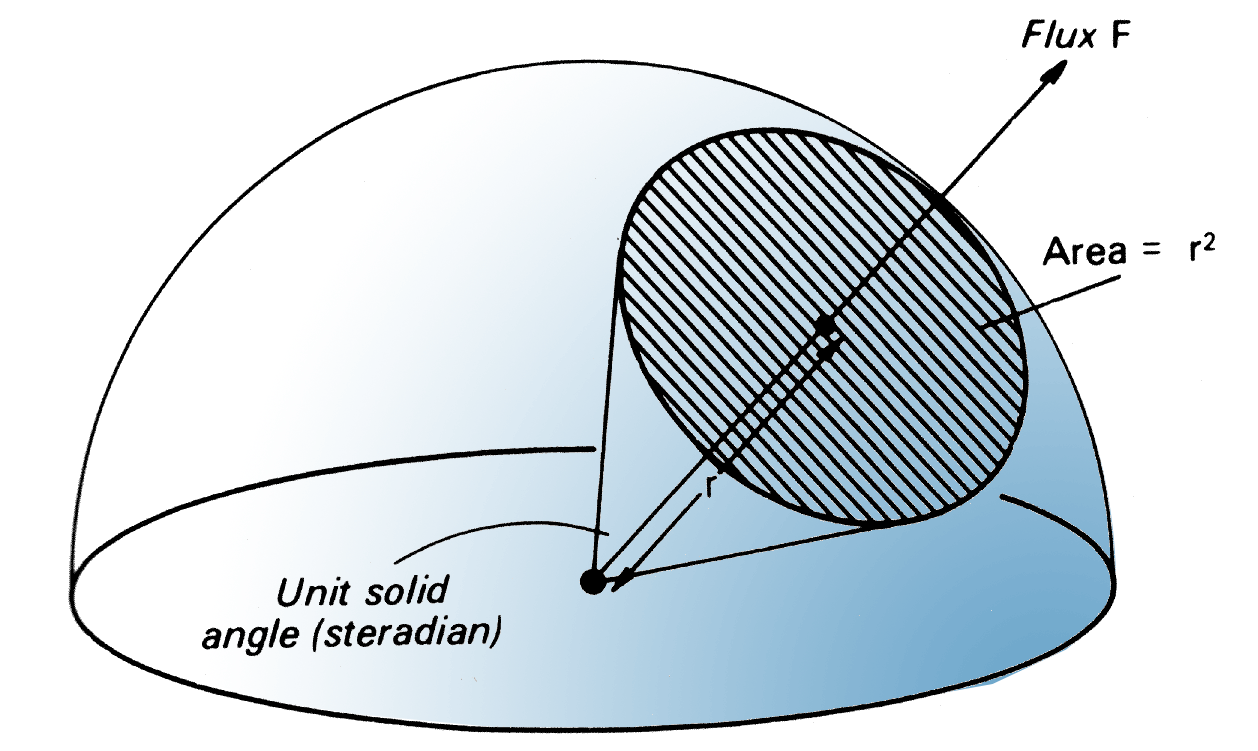
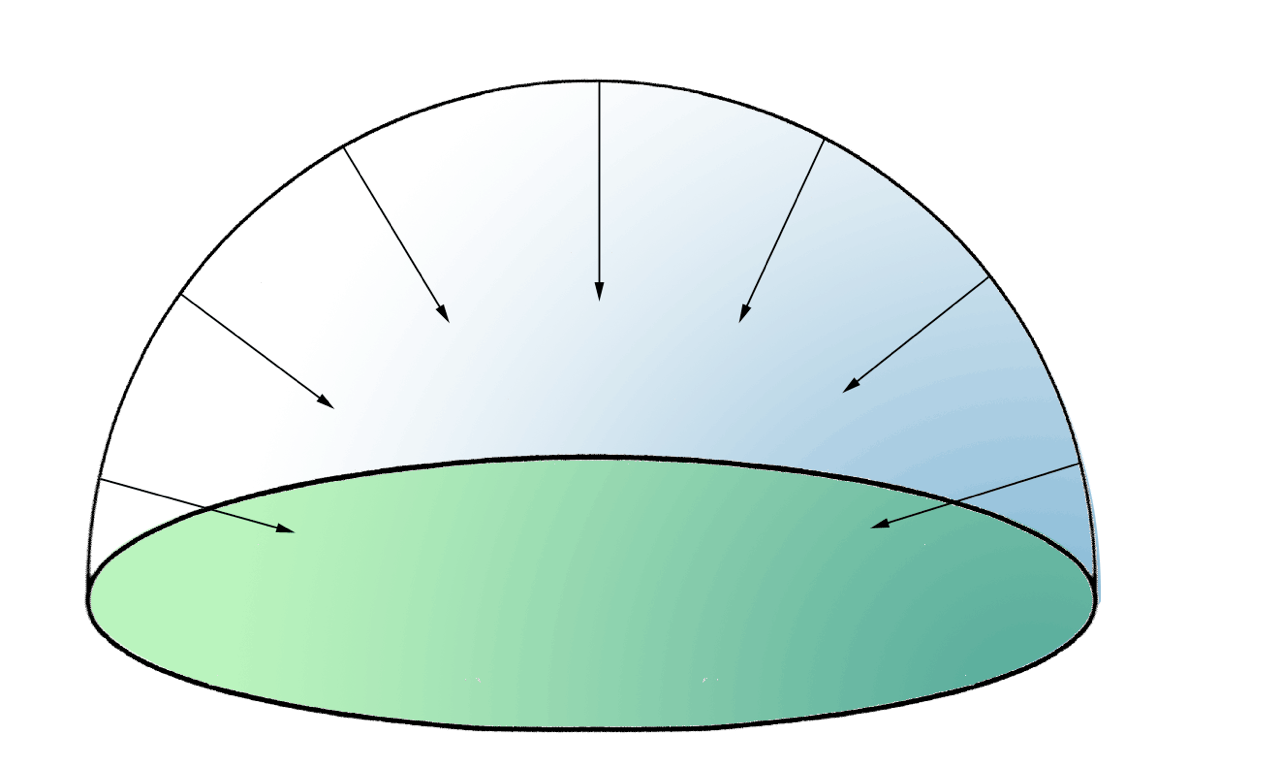
Irradiance is the total radiant flux from \(2\pi sr\) reaching a unit area of a given surface with units W m^-2.

Radiant intensity can be defined as the amount of power emitted by a source in a particular direction per unit solid angle. (directional) Solar Irradiance is a measure of how much solar power you are getting at your location. (hemispherical)

Next time: Consider the power (P) being emitted from a source which is directed in a particular direction along the center of a cone that encompasses the solid angle, the radiant intensity is equal to the emitted power. 

Example: https://www.mathsisfun.com/geometry/steradian.html

Definitions

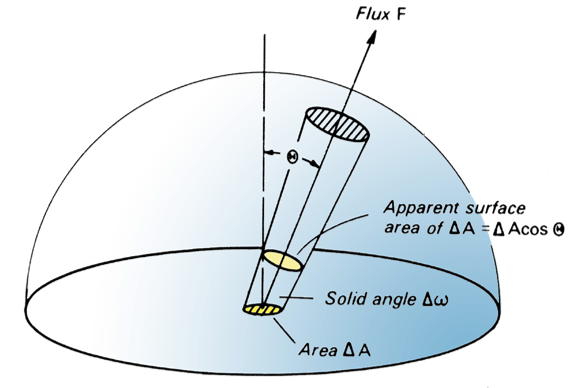
Radiance is the radiation flux per unit solid angle per unit projected source area (\(\Delta A \cos(\theta)\)) of an area \(\Delta A\). Its unit is W m^-2 sr^-1

Radiance at Totem Field UBC (Oke, 1987)

Builds on Radiant intensity (W sr-1) You can think that power arriving at a grazing angle is “smeared out” over a larger surface

Direct and Diffuse Irradiance

• Direct (S): comes directly in parallel rays from Sun.
• Diffuse (D): after scattering and reflection by the Earth’s atmosphere and nearby objects.

Measuring Solar Irradiance

• Pyrheliometer
  • Measures direct irradiance
• Pyranometer
  • Measures direct+diffuse irradiance

Pyranometer: solar radiation flux density  Wm-2

Measuring Solar Irradiance

• Diffusometer
  • Measures diffuse irradiance because shaded

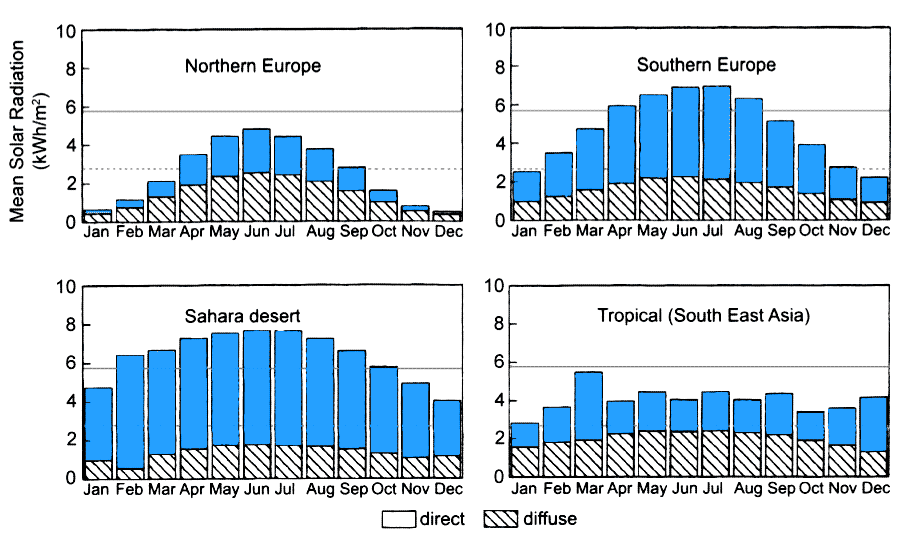
Distribution of direct and diffuse radiation

kilowatts multiplied by the time in hours Discussion of this figure

Summary of Terminology

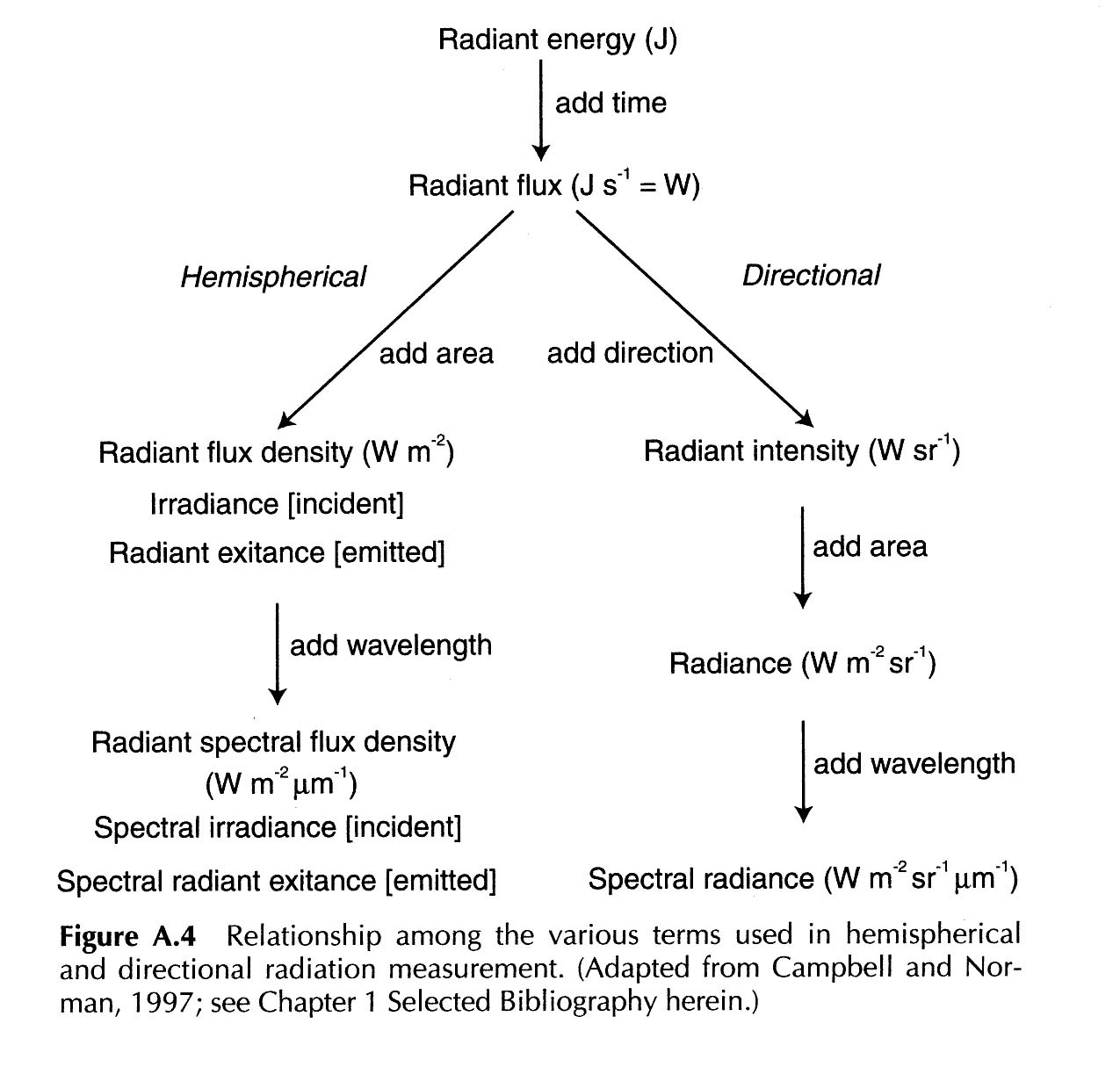
Relationship among the various terms used in hemispherical and directional radiation measurements (Adapted from Campbell and Norman, 1997)

-Read textbook!

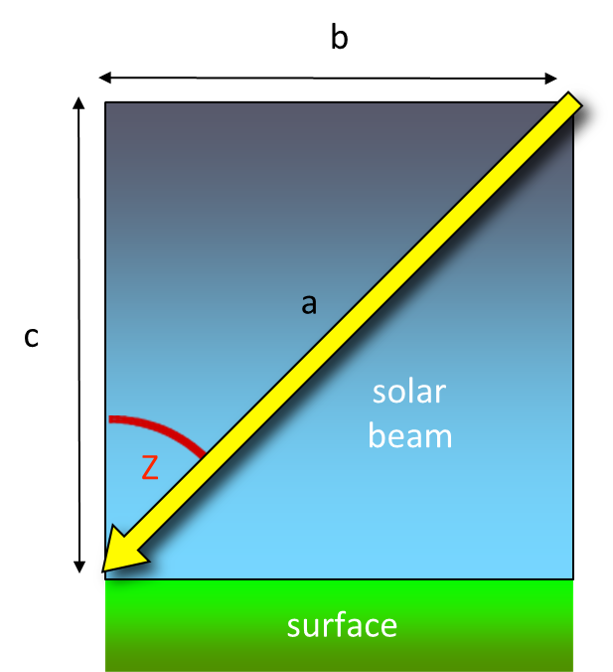
Calculation of \(SW_\downarrow\) - slab approach

Bulk transmissivity of the atmosphere (\(\Psi_a\)) depends on turbidity of the air (scattering + absorption) and path length trough the atmosphere.

\[ SW_\downarrow = I_{ex} \Psi_a^{m} \qquad(2)\]

where

\[ m = \small\frac{1}{\cos(Z)} = \small\frac{1}{\sin(\beta)} \]

• \(\Psi_a\) varies from about 0.9 (clean) to 0.6 (dirty, smog)

m = 1/cos(Z); so the greater the solar zenith angle, the greater the optical air mass, and the more attenuated the radiation at the surface. To account for the effects of altitude values of m should be multiplied by the ratio of the station atmospheric pressure to that at standard sea-level (101.3 kPa). Start with https://ibis.geog.ubc.ca/courses/geob300/applets/latitude/index.html

Test your knowledge (iClicker)

Assuming that \(I_ex\) is 450 W m^-2, \(\Psi_a\) = 0.84, and Z = 57.3 \(^\circ\), what is \(SW_\downarrow\)?

I_ex = 450 #W m-2
Psi_a = 0.84
Z = 57.3 #deg
Z=Z*pi/180 # convert to radians

Test your knowledge (iClicker)

Assuming that \(I_ex\) is 450 W m^-2, \(\Psi_a\) = 0.84, and Z = 57.3\(^\circ\), what is \(SW_\downarrow\)?

I_ex = 450 #W m-2
Psi_a = 0.84
Z = 57.3 #deg
Z=Z*pi/180 # convert to radians
SW_down = I_ex*Psi_a^(1/cos(Z))
sprintf('%s W m^-2',SW_down)

[1] "325.875226835139 W m^-2"

Physically based calculation of \(SW_\downarrow\)

Models attempt (with varying degrees of completeness) to account for all physical processes in the chain:

\(I_0 -> I_ex -> SW_\downarrow^1 -> SW_\downarrow^2 -> SW_\downarrow^3\)

1. Cloudless, horizontal surface

2. Cloudy, horizontal surface

3. Sloping terrain

I0 = the solar constant Kex = at the top of the atmosphere (Extraterrestrial irradiance) Computer code for the prediction and analysis of optical measurements through the atmosphere.

\(\Psi_a = 0.8\)

\(\Psi_a = 0.58\)

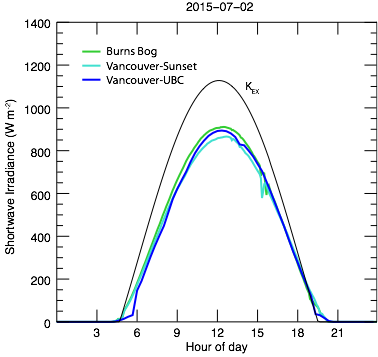
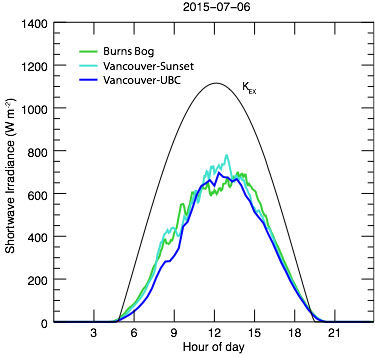
Effect of Forest Fire Smoke

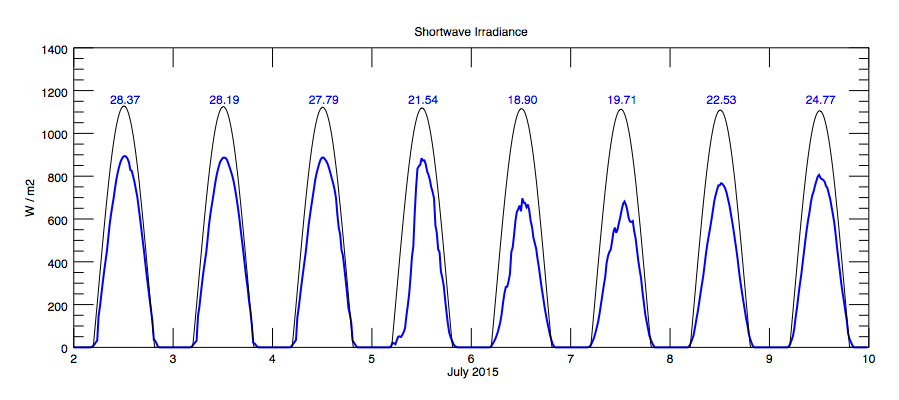
Effect of Forest Fire Smoke

Clear Skies

Smoky Skies

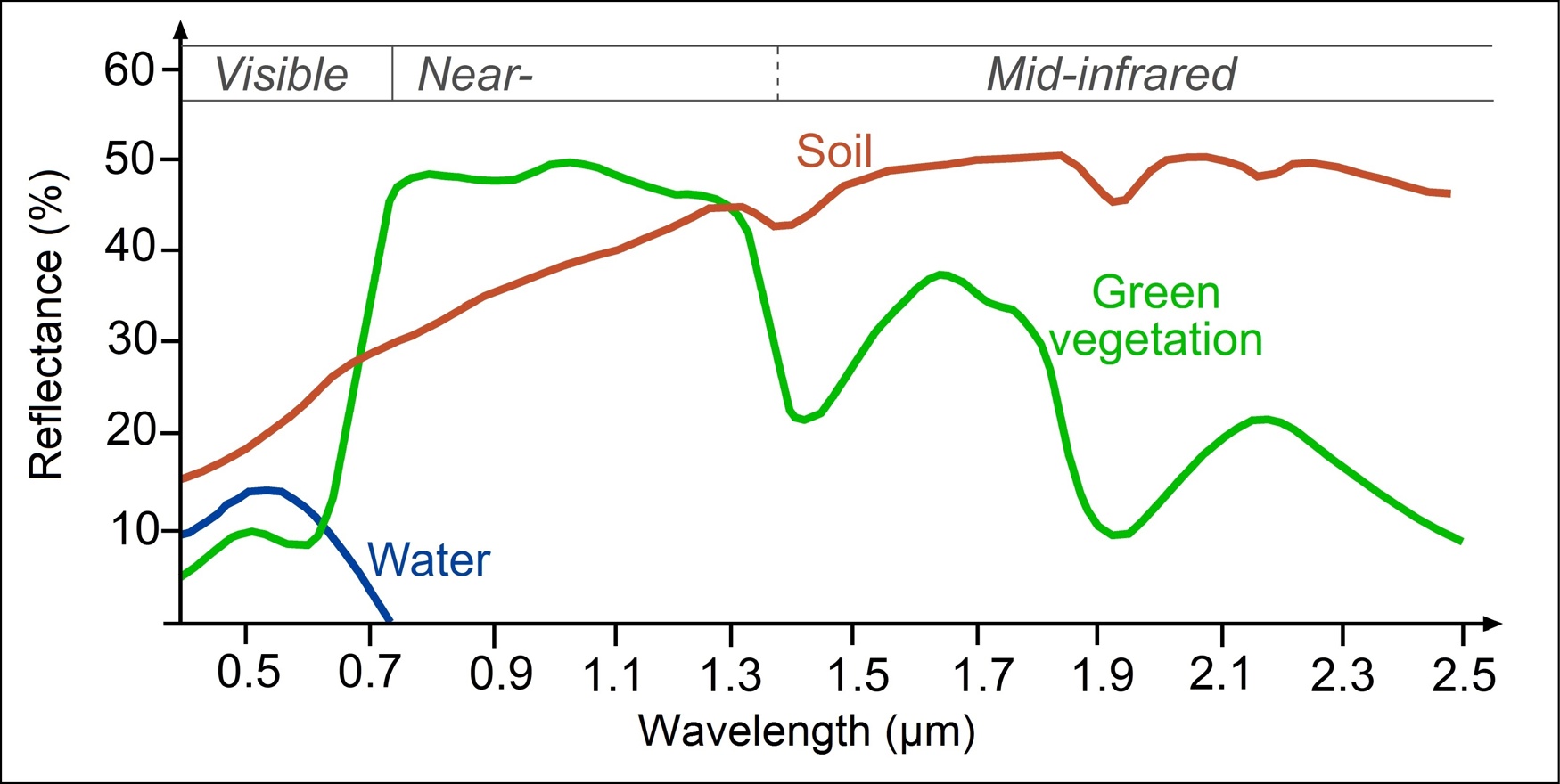
Reflectivity and Reflection Coefficient

Spectral reflectivity \(\alpha_\lambda\) relates to a single wavelength. The reflection coefficient is the average reflectivity across a wavelength band weighted by Irradiance for that band \(\alpha_{\lambda_1 \rightarrow \lambda_2}\)

Reflectivity is the fraction of incident radiation reflected by a surface The reflectance characteristics of Earth’s surface features may be quantified by measuring the portion of incident energy that is reflected This is measured as a function of wavelength (λ) and is called spectral reflectance (rλ ) Water (in soil, vegetation or water bodies) absorbs radiation at near-IR wavelengths and beyond (strong absorption bands at about 1.4, 1.9 and 2.7 μm)

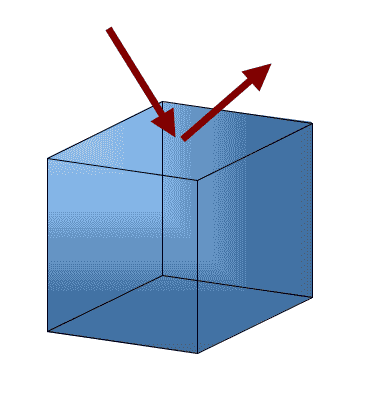
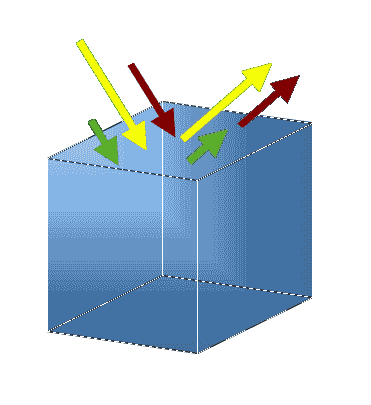
Reflectivity and Reflection Coefficient

\[ \alpha_\lambda = \frac{\lambda_{reflected}}{\lambda_{incident}} \qquad(3)\]

\[ \alpha_{\lambda_1 \rightarrow \lambda_2} = \frac{\int_{\lambda_1}^{\lambda_2}\alpha_\lambda I_\lambda d_\lambda}{\int_{\lambda_1}^{\lambda_2}I_\lambda d_\lambda} \qquad(4)\]

• When \(\alpha_{\lambda_1 \rightarrow \lambda_2} = \alpha_{\lambda\ = 0.15 \mu m \rightarrow \lambda_2 = 3 \mu m}\); we call it surface albedo \(\alpha\).

Spectral Reflectivity of a Leaf (iClicker)

What does the highlighted (green) area on the chart below represent?

Middle is absorptivity The relative roles of reflectivity (αλ), transmissivity (ψλ) and absorptivity (ζλ) are governed by the structure of the leaf interior and the radiative properties of the main plant pigments (especially chlorophyll) Absorb in the blue (0.40-0.51) and red (0.61-0.70); the waveband between 0.40 and 0.70 μm is therefore designated as photosynthetically active radiation (PAR) αλ decreases with increasing water content. The strong absorption bands at 1.45 and 1.95 μm are due to water. On the other hand, in the near infrared (NIR) high reflectivity enables the leaf to reject the bulk of the incident energy. The heat content of this radiation is very high but it is not useful for photosynthesis, therefore its rejection is helpful in offsetting the heat load on the leaf.

The high emissivity at longer wavelengths also helps the leaf to shed heat to the environment and keep leaf temperatures moderate. The cellular structure tends to cause almost totally diffuse scattering. This results in almost = portions of the radiation being reflected back & transmitted on through the leaf and explains why the αλ and ψλ curves in Figure 2 are similar in shape

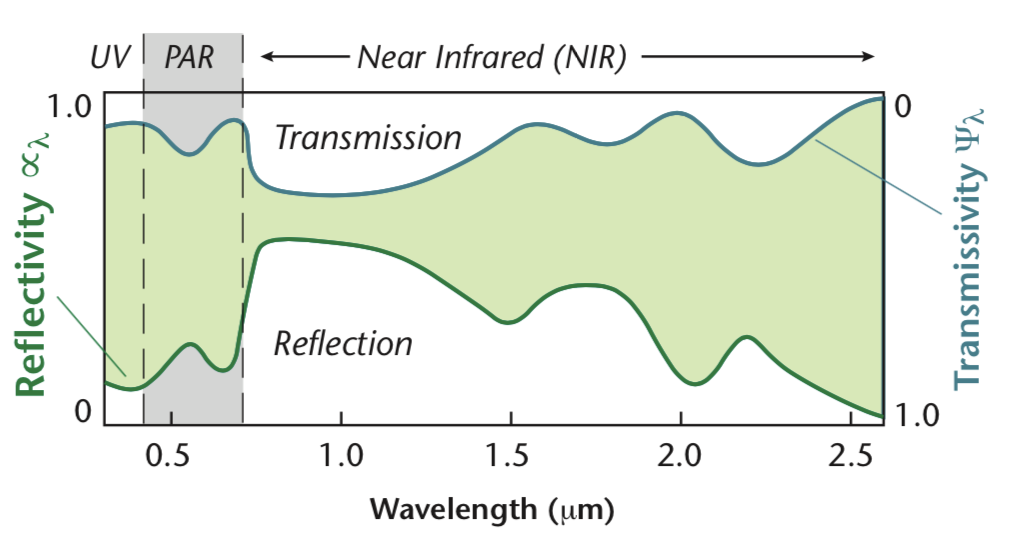
Healthy vs. Unhealthy Vegetation

A plant with more chlorophyll will reflect more near-infrared energy than an unhealthy plant. 

Normalized Difference Vegetation Index

\[ NDVI = \frac{NIR-Red}{NIR+Red} \qquad(5)\]

NDVI itself thus varies between -1.0 and +1.0.

NDVI as an indicator of drought

The above image shows the NDVI anomaly in the U.S. for August 1993. In that year, heavy rain in the Northern Great Plains (North and South Dakota, Alberta, and Saskatchewan) led to flooding in the Missouri River. The resulting exceptionally lush vegetation appears as a positive anomaly (green). Concurrently, in the Eastern U.S., rainfall was very low, and the region exhibited a strong negative anomaly (dark red).

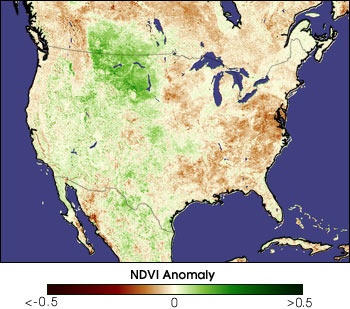
Albedo

The albedo \(\alpha\) can be simply measured as the fraction of incident solar radiation reflected by a surface.

Albedo

The albedo \(\alpha\) can be simply measured as the fraction of incident solar radiation reflected by a surface.

Albedo

Shown are typical values. Individual values vary widely. * for small zenith angles Z only.

• Albedo is a very significant surface variable to microclimate because it controls the absorption of the main source of energy by day.
• Albedo has a strong influence on the climate system. Adjacent surfaces receive the same amount of K↓ but the impact is determined by .

Table 1: CAPTION

Surface	X alpha
Fresh snow	0.95
Old snow	0.40
Short grass	0.25
Crops	0.20
Deciduous Forests	0.20
Coniferous Forests	0.10
Water *	0.05

Shortwave Reflection Creates Energetic Differences

U = urban, S = suburban, R = rural (grass, crops)

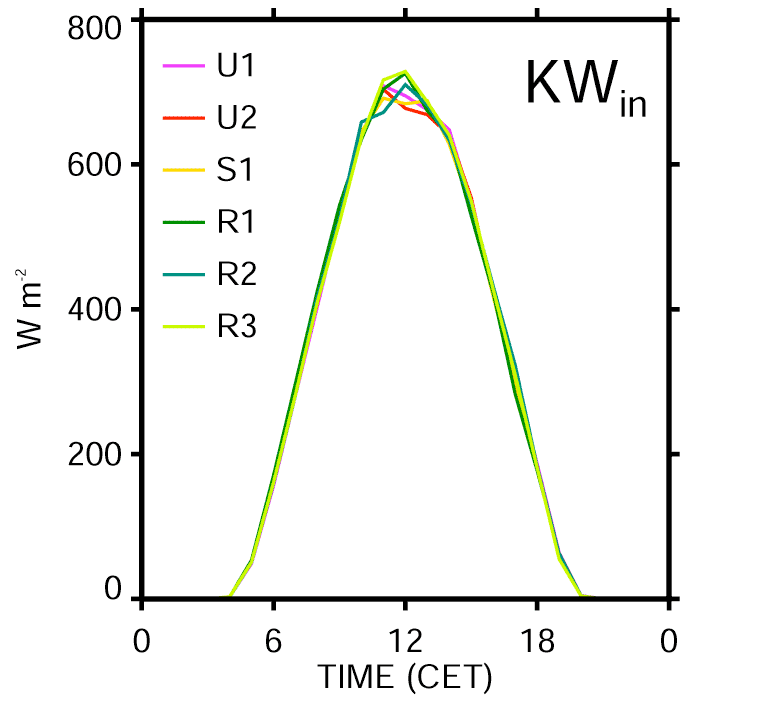
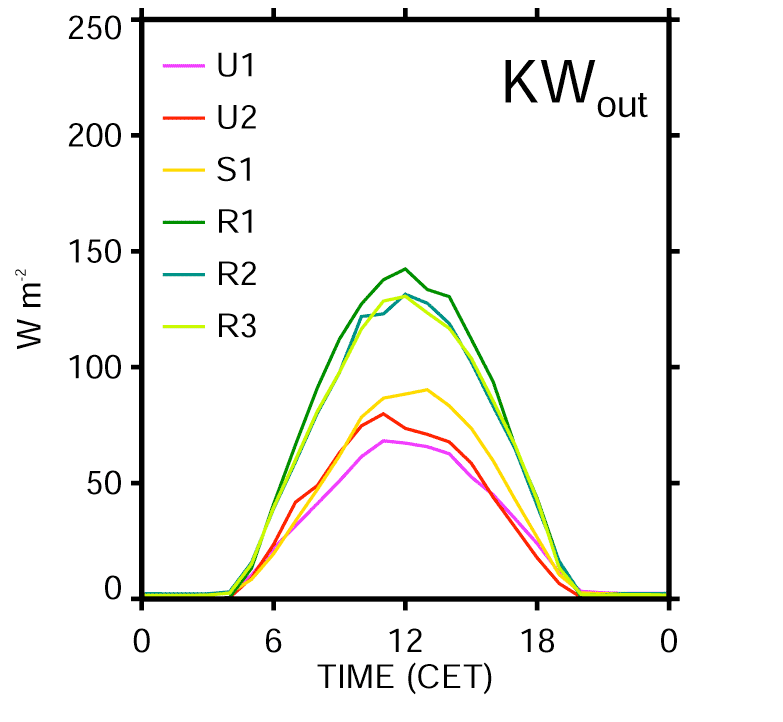
Albedo and Canopy Structure

• Increased “trapping” of solar radiation with increased height/thickness (multiple reflections)
• Individual leaves generally have higher reflectivity than a canopy of the same leaves

The albedo (α) of a vegetation stand is lower than the value for its individual leaves because reflection depends not only on the radiative properties of the component surfaces, but also upon the stand architecture and the angle of solar incidence. The latter two factors control the amount of penetration, radiation trapping, and mutual shading within the stand volume. Thus although most leaves have an albedo of about 0.30 the albedo of crops and other vegetation communities is less, and to some extent a function of their height. For most agricultural crops and natural vegetation less than 1 m in height the albedo lies in the remarkably narrow range from 0.18 to 0.25.

Albedo and Canopy Structure

• Albedo depends on canopy structure
  • Increased “trapping” of solar radiation with increased height/thickness (multiple reflections)
  • Individual leaves generally have higher reflectivity than a canopy of the same leaves.

Short-wave radiation budget of (a) an orange orchard, and (b) a single-layer mosaic of fresh orange leaves. All values expressed as percentages of the incident radiation (after Kalma, 1970). Hence the natural orientation of leaves and the depth of the canopy greatly enhance absorption due to trapping as a result of multiple internal reflection.

Albedo Depends on Leaf State and Canopy Height

While albedo decreases with height, it also is strongly influenced by leaf state & vegetation cover (ie. patchiness).

Snow/Ice Cover is a Significant Control

Ice-albedo feedback

Specular and Diffuse Reflection

Specular: beam reflected at same angle (like mirror)

Diffuse: beam diffused isotropically (Lambertian)

For short-wave beam radiation (S) most natural surfaces act as diffuse reflectors for solar elevation angle greater than 30◦ but may become increasingly specular for smaller angles. This is especially true for relatively smooth surfaces such as water, ice, snow, etc. Natural surfaces show very little directionality for diffuse radiation (D). Lambertian reflection: The apparent brightness of a Lambertian surface to an observer is the same regardless of the observer’s angle of view.

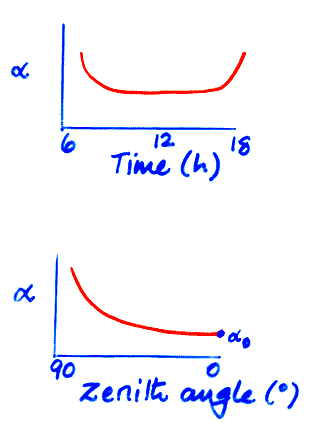
Albedo as a Function of Solar Altitude

Early morning and evening albedos are higher, and when plotted versus the position of the Sun in the sky show a characteristic curve (Figure 3). higher probability that photons can leave the snowpack if they hit the surface at grazing angles. The diurnal variation of the albedo is much less with cloudy skies.

Its role in explaining seasonal variations of albedo is obscured by changes in plant phenology, snow, etc. However, since the highest albedos occur at the times of low energy input the effect of this diurnal variation on the total radiation budget is small. This dependence upon the solar altitude also explains why tropical albedos are usually less than those for similar surfaces at higher latitudes, and accounts for the observation that the diurnal variation of the albedo is much less with cloudy skies.

This-pair-share: to get a robust estimate of α, students can either take the value at noon, the median value of the entire day, or do an average for a subset around midday. Also acceptable is the use of the daily totals or sums, i.e. α = sumK ↑ /sumK ↓.

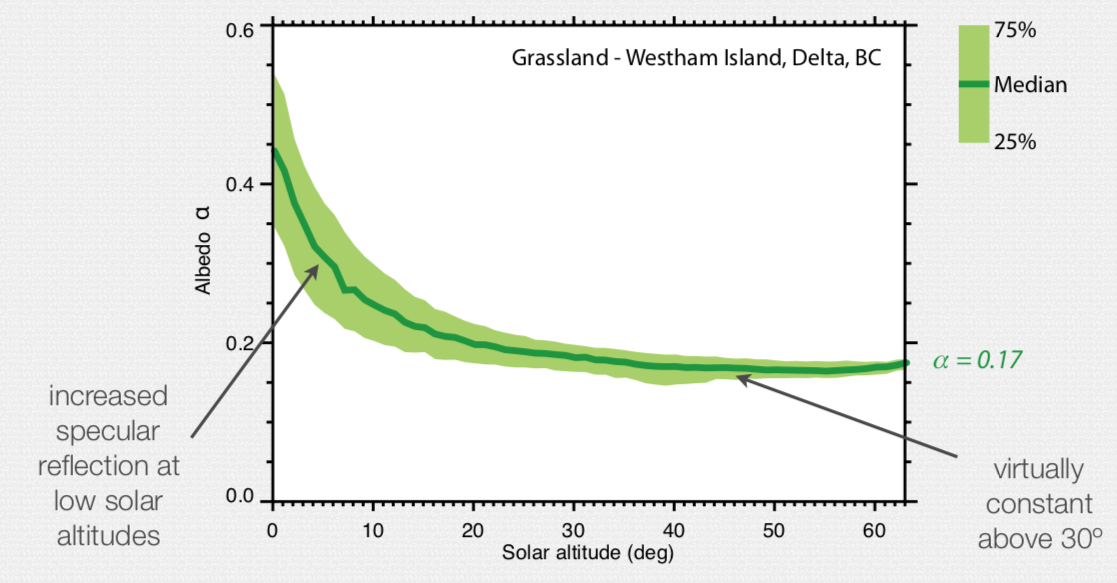
Albedo as a Function of Solar Altitude

• Natural surfaces seem to diffuse for Z < 60°, and increasingly specular as Z → 90°. As a simple model we might use:

\[ \alpha_Z = \alpha_0 + (1-\alpha_0)\exp^{-0.1 Z} \]

• Values in literature usually refer to the mid-day albedo, or albedo calculated from daily totals

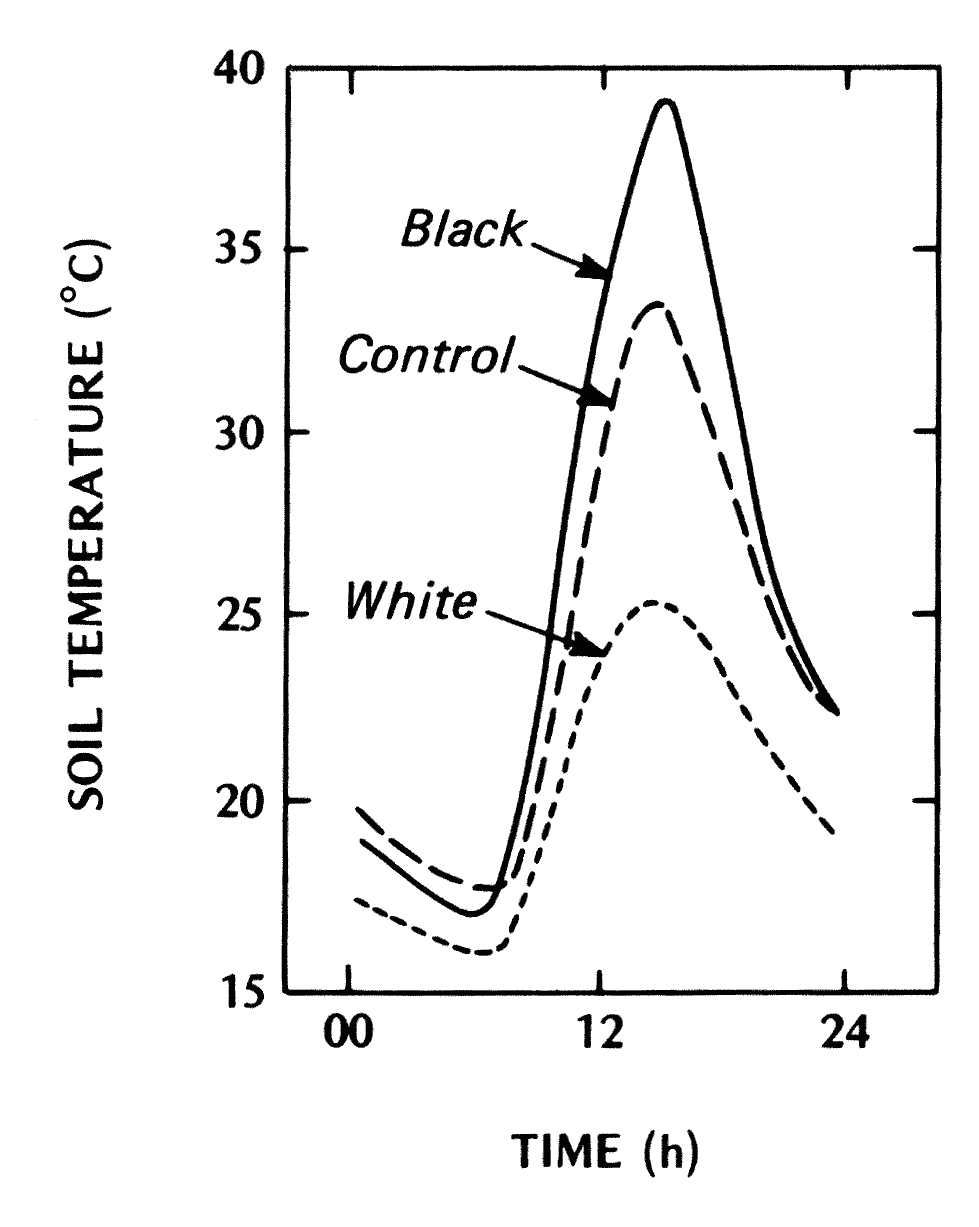
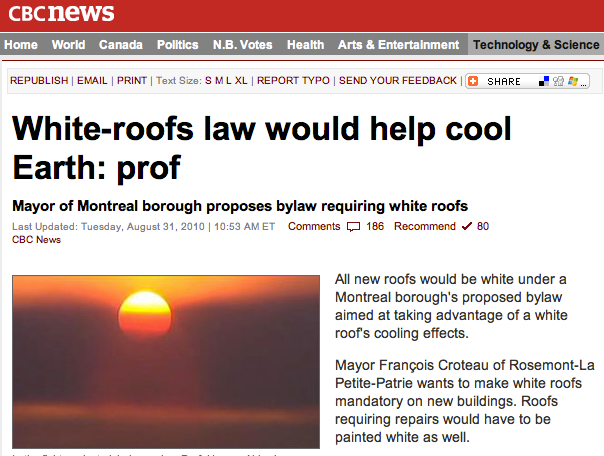
Modifying Reflectivity

There are mainly two ways to modify the short-wave radiative surface properties:

1. Reflectivity control: Changing the surface color in various wavelengths by painting the surface (e.g. roof-tops), or wrapping the surface in white or dark plastic (agriculture).
2. Geometry control: Changing the microtopographic feature of a setting to increase or reduce absorption.

Albedo control

Reflectivity and Geometry Control

Take home points

• As short-wave radiation passes through the atmosphere, it is reflected, scattered and absorbed.
• At the surface, we therefore experience diffuse irradiance in addition direct-beam irradiance.
• The transmission of direct-beam radiation can be described by a slab approach using a bulk atmospheric transmissivity.
• As short-wave radiation reaches a surface, part of it is reflected - can be quantified by spectral reflectivity and the reflection coefficient (called albedo for short-wave)
• Albedo is controlled by the material, 3D form, the leaf state and the presence of snow.
• Reflection can be specular and/or diffuse - and most natural surfaces become increasingly specular at low solar altitudes.
• Changing the albedo of a surface (material, geometry) is a powerful tool to microclimate modification.