Surface Energy Balance

Surface Energy Balance

Today’s learning objectives

• Define the energy balance equation for an ideal surface.
• Describe how energy fluxes vary between daytime and nighttime.
• Define the Bowen ratio.
• Explain when can we reduce a 3D land-atmosphere interface to 1D.

Why are we interested in the ‘surface’?

• Ultimate goal: Predicting and managing surface-atmosphere interactions.

• Quantifying the impact of one system on another one.

• Understanding a system’s interior dynamics (black box).

• Boundary condition:

  • Lower boundary condition for the ABL
  • Upper boundary for soil climates
  • Outer boundary for organisms and buildings

Boundary conditions apply constraints on solutions to equations that are motivated by the physical problem being considered. Both ordinary and partial differential equations need boundary conditions to be solved.

Types of Surface-Atmosphere Interfaces

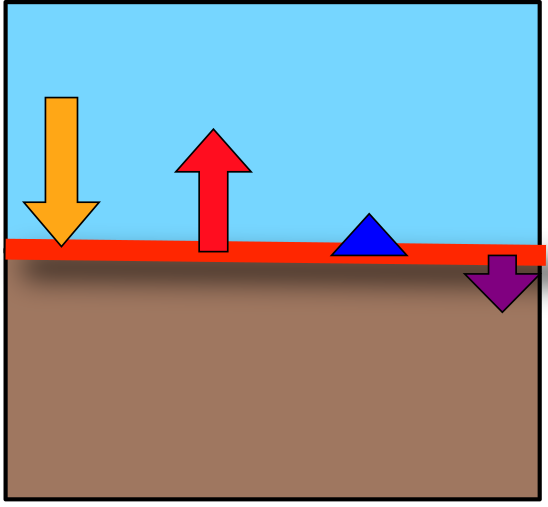
Simple, homogenous bare soil/rock surface

Types of Surface-Atmosphere Interfaces

Complex, vegetated surface (e.g., a forest canopy)

Types of Surface-Atmosphere Interfaces

“Two-dimensional”, semi-transparent surface (e.g., a leaf)

Types of Surface-Atmosphere Interfaces

Three-dimensional volume (e.g., an animal)

Flat land-atmosphere (solid-fluid) interface with no mass. Example: Bare soil. Three-dimensional land-atmosphere interface with mass within the interface (air, vegetation, …). Example: Forest. Flat two-dimensional object without mass (solid) within a fluid (atmosphere or water). Example: Leaf. A three dimensional volume with mass surrounded by the fluid (atmosphere or water). Example: Animal.

Energy Fluxes at Earth’s Surface

• ‘Ideal’ surface considered here is smooth, horizontal, homogeneous, extensive, and opaque to radiation.
• Only vertical fluxes need to be considered.
• The storage term is dropped \(\Delta S=0\)

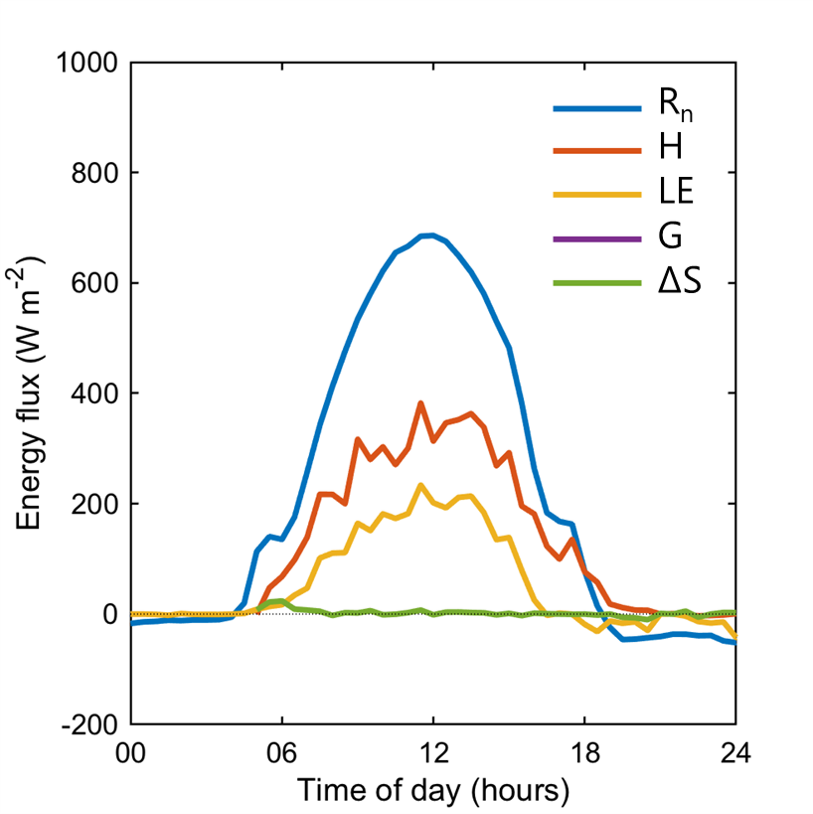
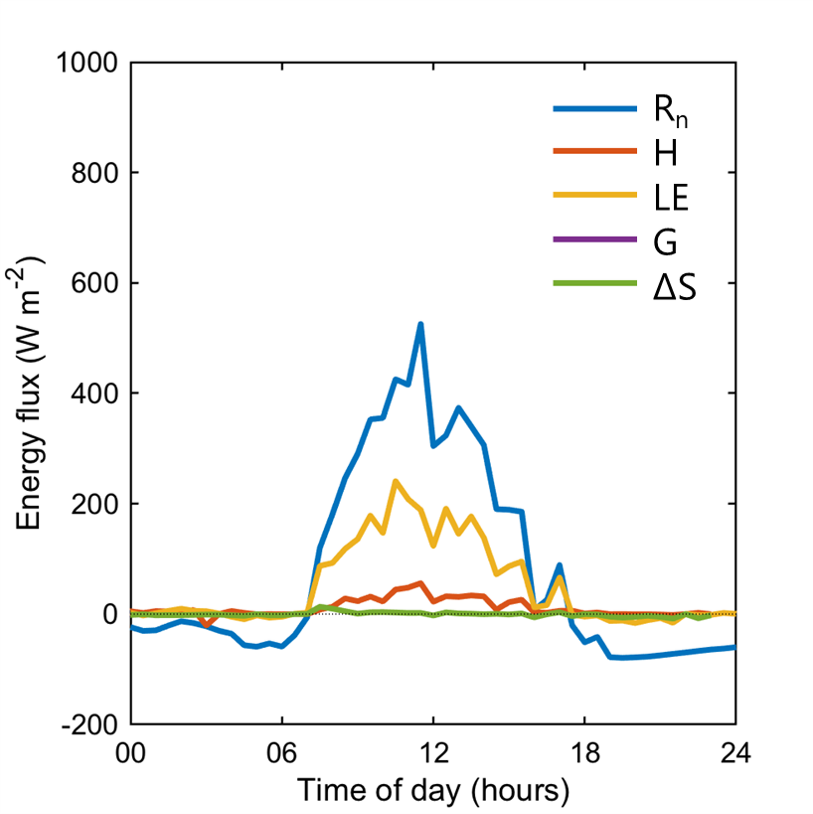
\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(1)\]

The net radiative flux is a result of the radiation balance at the surface, which will be discussed in more detail in a few lectures. Daytime dominated by the solar radiation (toward the surface), at night the net radiation is much weaker & away from the surface. The surface warms up during the daytime, while it cools during the evening and night hours. Sensible (direct) heat flux - arises as a result of the difference in the temperatures of the surface and the air above. > few millimeters (the thickness of the molecular sublayer), the primary mode of heat exchange becomes advection or convection involving air motions. Thus, the heat flux is down the average temperature gradient. latent heat or water vapor flux is a result of evaporation, evapotranspiration, or condensation at the surface. Nevertheless, evaporation results in some cooling of the surface, which in the surface energy budget is represented by the latent heat flux from the surface to the air above. heat exchange through the ground medium is primarily due to conduction if the medium is soil, rock, or concrete. Through water, however, heat is transferred first by conduction in the top few millimeters (molecular sublayer) from the surface and then by advection or convection in the deeper layers (surface layer, mixed layer, etc.) of water in motion. The depth of the submedium, which responds to and is affected by changes in the energy fluxes at the surface on a diurnal basis, is typically less than a meter for land surfaces and several tens of meters for lakes and oceans.

This equation describes how the net radiation at the surface must be balanced by a combination of the sensible and latent heat fluxes to the air and the heat flux to the subsurface medium.

Sign Convention

• All the radiative fluxes directed toward the surface are positive.
• Non-radiative energy fluxes directed away from the surface are positive.
  • Each component is on an interval scale

\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(2)\]

Sign Convention (iClicker)

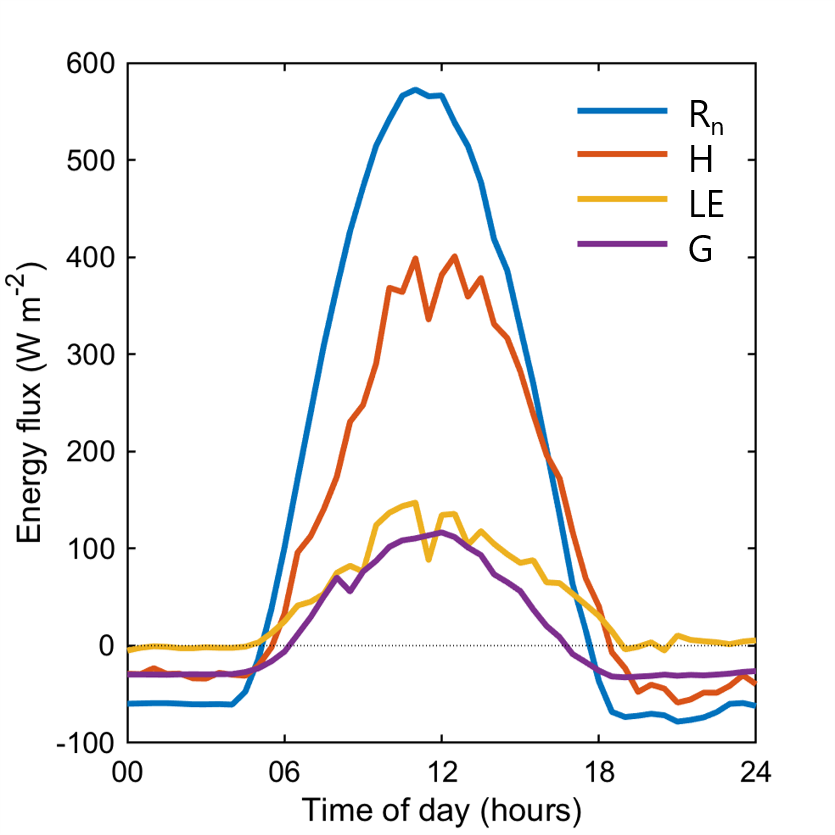
Which component(s) of the energy balance can take negative values?

• Net-Radiation
• Sensible & Latent Heat Flux
• Ground Heat Flux
• All of the above
• None of the above

Daytime

• Typically:
  • \(R_n\) > 0
  • \(H\), \(LE\), and \(G\) > 0
• There are plenty of exceptions

\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(3)\]

During the daytime, the surface receives radiative energy (Q*> 0), which is partitioned into sensible and latent heat fluxes to the atmosphere and the heat flux to the submedium. Typically, QH, QE, and QG are all positive over land surfaces during the day.

Actual magnitudes of the various components of the surface energy budget depend on many factors, such as the type of surface and its characteristics (soil moisture, texture, vegetation, etc.), geographical location, month or season, time of day, and weather.

Nighttime

• Typically:
  • \(R_n\) < 0
  • \(H\), \(LE\), and \(G\) < 0
• There are plenty of exceptions

\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(4)\]

At night, the surface loses energy by outgoing radiation, especially during clear or partially overcast conditions. This loss is compensated by gains of heat from air and soil media and, at times, from the latent heat of condensation released during the process of dew formation. All the terms of the surface energy balance for land surfaces are usually negative during the evening and nighttime periods. Their magnitudes are generally much smaller than the magnitudes of the daytime fluxes, except for QG. The magnitudes of QG do not differ widely between day and night, although the direction or sign obviously reverses. One can interpret the EB equation in terms of the partitioning of net radiation into other fluxes. The net radiation may be considered an external forcing, while the sensible, latent and ground heat fluxes are responses to this radiative forcing.

Bowen Ratio

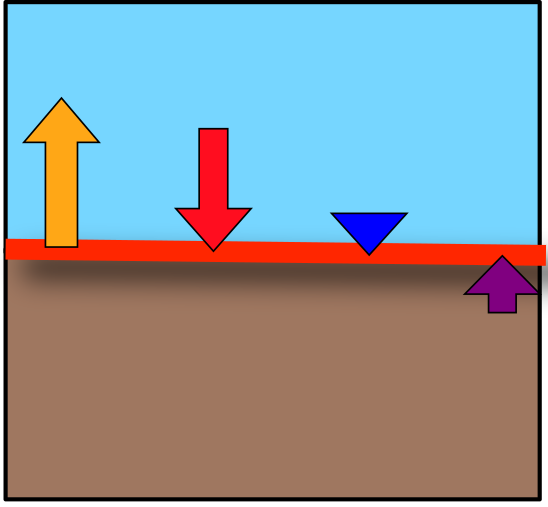
The Bowen Ratio (\(B\)) is used to express the partitioning of net radiation at a surface.

\[ B = \frac{H}{LE} \qquad(5)\]

\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(6)\]

The Bowen Ratio (B) is used to express the partitioning of net radiation at a surface. B<<1 for lakes, rice paddies, well irrigated fields; whereas the B is much larger for dry surfaces (Desert, Urban)

Bowen Ratio (iClicker)

On a hot sunny day, which surface would you expect to have the largest Bowen Ratio?

• The Ocean
• Ice Sheet
• A Wheat Field
• A Pine Forest
• Desert Sand

\[ B = \frac{H}{LE} \qquad(7)\]

Bowen Ratio Method

\[ B = \frac{H}{LE} \qquad(8)\]

\[ LE = \frac{R_n-G}{1+B} \qquad(9)\]

\[ H = \frac{R_n-G}{1+B^{-1}} \qquad(10)\]

\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} \qquad(11)\]

The simple relationship between the ground heat flux and net radiation allows for the sum of the sensible and latent heat fluxes to be easily determined from the measurement or calculation of net radiation. Further separation of the total heat flux into sensible and latent components can be made if the Bowen ratio, can be estimated independently (e.g., using the Bowen ratio method to be discussed later). B = measure vertical heat and vapor gradients

Bowen Ratio Method

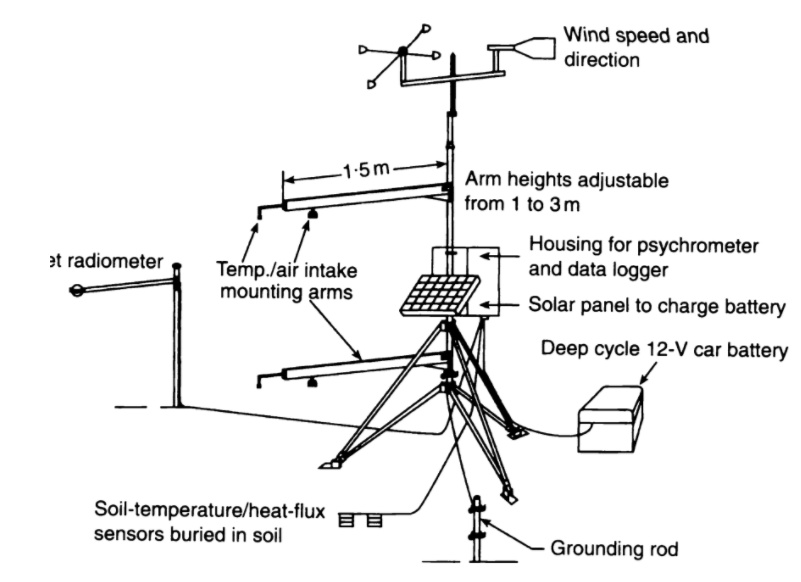
Assuming \(B= 5.0\) with daytime \(R_n = 250 \rm{W m^{-2}}\) & \(B = 75 \rm{W m^{-2}}\), estimate \(\rm{LE}\) & \(\rm{H}\).

def Bowen_Method(B,R_n,G):
  H = (R_n-G)/(1+B**-1)
  LE = (R_n-G)/(1+B)
  return(H,LE)

H,LE=Bowen_Method(5.0,250.0,75.0)

print(f'H = {H:.2f} & LE {LE:.2f} W m^-2')

H = 145.83 & LE 29.17 W m^-2

Bowen Ratio Method

Assuming \(B= 4.0\) with daytime \(R_n = -55 \rm{W m^{-2}}\) & \(B = -25 \rm{W m^{-2}}\), estimate \(\rm{LE}\) & \(\rm{H}\).

Bowen_Method<- function(B,R_n,G){
  H = (R_n-G)/(1+B**-1)
  LE = (R_n-G)/(1+B)
  return(c(H,LE))
}

out=Bowen_Method(4.0,-55.0,-25.0)

sprintf('H = {%.2f} & LE {%.2f} W m^-2',out[1],out[2])

[1] "H = {-24.00} & LE {-6.00} W m^-2"

When The Method Fails

This method relies on the assumption of Homogeneity.

• Rough or irregular surfaces violate that assumption.

When The Method Fails

This method relies on the assumption of Homogeneity.

• Rough or irregular surfaces violate that assumption.

Photo: A. Christen

Adding A Storage Term

When dealing with more complex, 3D volumes:

• We need to account for the storage
• Energy can be stored above and below the surface

-More realistic to consider a volume.

Adding A Storage Term

• Net chemical energy & sensible heat storage in biomass
• Net sensible & latent heat storage in canopy air
• Net sensible heat storage in structures

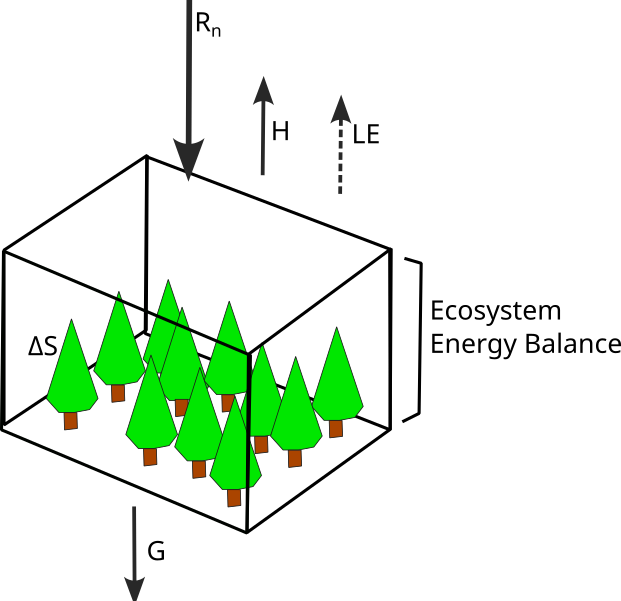
\[ \color{orange}{R_n} = \color{red}{H} + \color{blue}{LE} + \color{purple}{G} + \color{green}{\Delta S} \qquad(12)\]

-More realistic to consider a volume.

Real world examples: Fallow rice field

Real world examples: Freshwater marsh

Wetting of the subsurface soil by precipitation or artificial irrigation can dramatically alter the surface energy balance, as well as the microclimate near the surface. The latent heat flux becomes an important or even dominant component of the surface energy balance, while the sensible heat flux to air is considerably reduced. The latter may even become negative during early periods of irrigation, particularly for small areas, due to advective effects. This is called the ‘oasis effect’ because it is similar to that of warm dry air blowing over a cool moist oasis. There is strong evaporation from the moist surface, resulting in cooling of the surface (due to latent heat transfer). The surface cooling causes a downward sensible heat flux from the warm air to the cool ground. Thus, QE is positive, while QH becomes negative, although much smaller in magnitude.

Real world examples: Deciduous shrub wetland

Magnitudes Highly Variable

Freshwater Marsh (California)

Shrub Wetland (Wisconsin)

Actual magnitudes of the various components of the surface energy budget depend on many factors, such as the type of surface and its characteristics (soil moisture, texture, vegetation, etc.), geographical location, month or season, time of day, and weather.

Magnitudes Highly Variable

Shrub Wetland (Spring)

Shrub Wetland (Summer)

Actual magnitudes of the various components of the surface energy budget depend on many factors, such as the type of surface and its characteristics (soil moisture, texture, vegetation, etc.), geographical location, month or season, time of day, and weather.

Energy Balance of a Leaf

• A surface within a single medium (e.g. a leaf surrounded by air).
• No third dimension, so heat storage is neglected.
• Energy flux densities on both sides have to be taken into account.
• Orientation of the surface is important for exchange processes (radiation).
• Storage of chemical energy

Energy Balance of a 3D Object

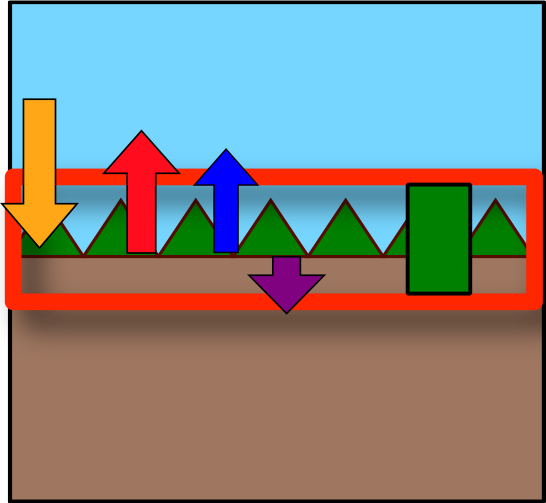
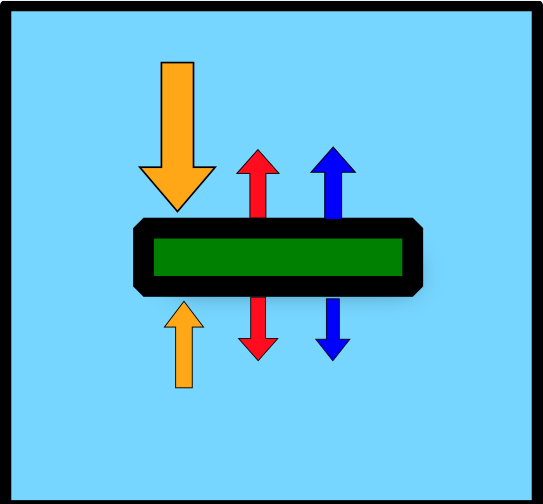
Usually an organism or object (animal, person, building) surrounded by air.

• Heat and mass storage in the interface has to be taken into account. In living organisms the metabolic heat plays a role. In some cases, anthropogenic heat (e.g. combustion processes) might be important.

Applications

• The energy budget over terrestrial surfaces is a key determinant of the land surface climate and governs a variety of physical, chemical and biological surface processes.
• Estimation of the rate of evaporation from bare ground and water surfaces and evapotranspiration from vegetative surfaces.
• Prediction of surface temperature.

Wang et al. 2015

The following list includes some of the applications of energy balance at or near the earth’s surface.

Take home points

• Land-atmosphere interfaces are complex boundaries, with significant energy and mass exchange.
• We covered the surface energy balance of (1) flat surfaces, (2) canopies, and (3) two-sided objects.
• The Bowen ratio of the ratio of sensible to latent heat.
• We explored how the surface energy budget varies by surface type and its characteristics (soil moisture, texture, vegetation, etc.), geographical location, month or season, time of day, and weather.