Energy and Mass Balances

Learning Objectives

• Describe how we can we track energy and mass in the atmosphere.
• Describe and simplify exchange processes of energy and mass at surface-atmosphere interfaces.
• Review: Define the dominant energy and mass transfer mechanisms in the atmosphere.

Conservation of Energy

One of the most powerful laws used in micrometeorology is the First Law of Thermodynamics.

• Energy cannot be created or destroyed by any ordinary means.
  • We can convert forms and move them around.

Conservation of Energy

Energy of relevant to climatology exists in the Earth-Atmosphere system in four different forms:

• Radiant: energy from electromagnetic radiation
  • All inputs inputs to/outputs from the Earth system are radiant
• Thermal: heat energy (both latent and sensible)
• Kinetic: energy associated with motion
• Potential: energy stored in an object due to it’s position or state

Conservation Laws

In general terms, we can define a conservation law as the balance between inputs, outputs, and storage (\(\Delta S\)) for a given system:

\[ In - Out = \Delta S \qquad(1)\]

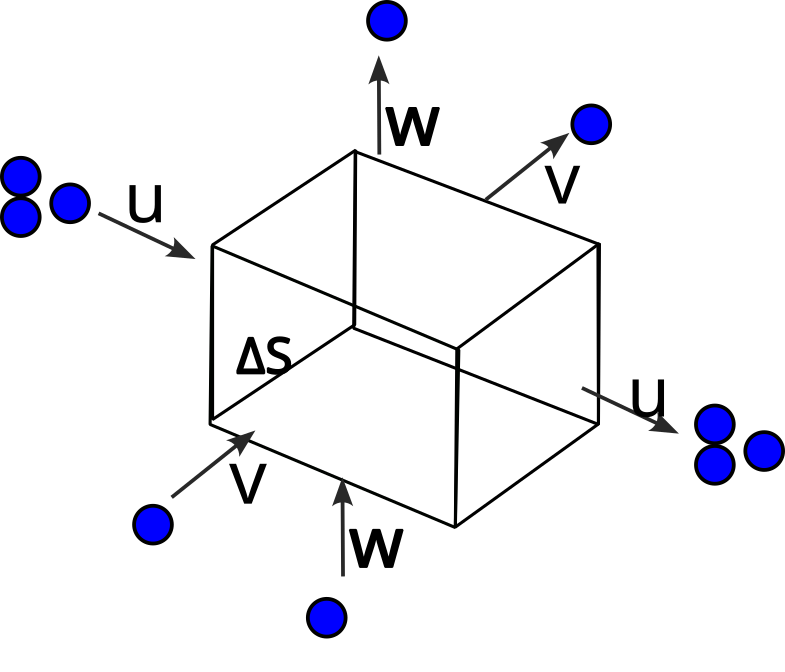
Conservation in 3D Space

In this case, \(\Delta S = 0\), because the inputs are balanced by the outputs.

In	Out	\(\Delta S\)
3u+1v+2w	3u+1v+2w	0

the sum of all sources (with sinks regarded as negative sources) gives the net flux out of a region. Divergence -> change in storage in our box is negative Convergence = change in storage in the box is positive

Negative divergence = This means a fluid flowing along the vector field defined by v would tend to become more dense at the point (x0, y0) Positive = the fluid flowing along the vector field becomes less dense around (x0, y0) Zero = no change in density

Source: https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/divergence-and-curl-articles/a/divergence

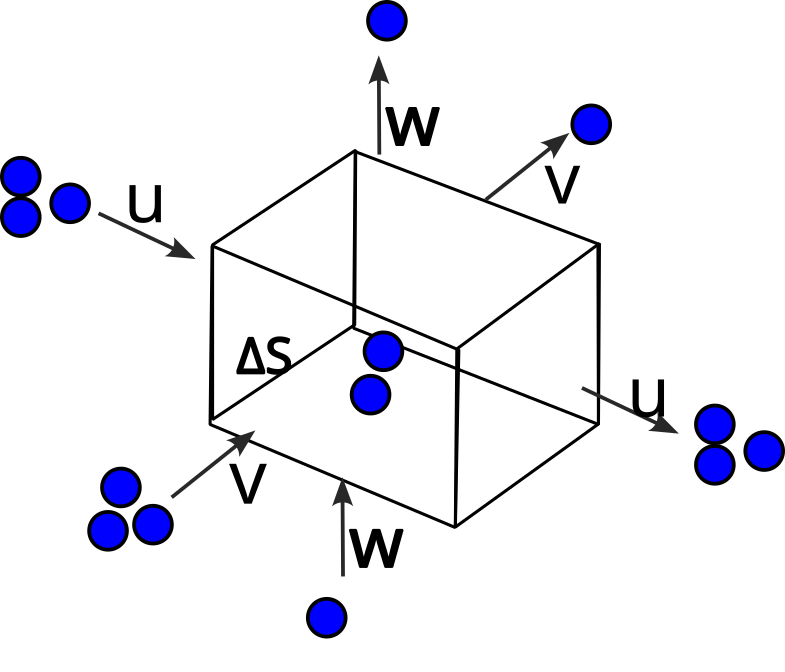
Convergence

In this case, we have convergence (\(\Delta S > 0\)) in the system, because the inputs exceed the outputs.

In	Out	\(\Delta S\)
3u+3v+1w	3u+1v+1w	2

Convergence

In this case, we have convergence (\(\Delta S > 0\)) in the system, because the inputs exceed the outputs.

• Convergence indicates accumulation over time. It could mean:
  • Air pressure increased
  • Absolute humidity increased
  • Heat energy increased due to warming

Divergence (iClicker)

In this case, we have divergence from the system, because the inputs to the system exceed the outputs from the system. What is the value of \(\Delta S\)?

In	Out	\(\Delta S\)
3u+1v+1w	3u+1v+3w	??

Divergence

In this case, we have divergence (\(\Delta S < 0\)) from the system, because the inputs to the system exceed the outputs from the system.

• Divergence indicates loss over time. It could mean:
  • Air pressure decreased
  • Absolute humidity decreased
  • Heat energy (e.g., temperature) decreased due to cooling

Conservation of a Scalar

Given some scalar \(c\), we can define it’s total change across a system \(\frac{dc}{dt}\) as the sum of it’s partial derivatives (\(\partial\)):

\[ \frac{dc}{dt} = \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + v \frac{\partial c}{\partial y} + w \frac{\partial c}{\partial z} \qquad(2)\]

• Advection: \(u \frac{\partial c}{\partial x}\), \(v \frac{\partial c}{\partial y}\), & \(w \frac{\partial c}{\partial z}\) represents the flow of c in to and out of the system
• Storage (\(\Delta S\)): \(\frac{\partial c}{\partial t}\) represents the change in c within the system over time

Partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary).

Spatial Variability (iClicker)

Which term would you use to describe the landscape in this photograph, where there are numerous types of vegetation present and complex topography with hills, ponds, and open ocean.

• Heterogeneous
• Homogeneous
• Homeopathic
• Polymorphic
• Static

Conservation at a land-interface

No wind can enter box from below; so transport from below is limited to diffusion from the soil.

In	Out	\(\Delta S\)
3u+1v+0w	2u+1v+3w	-2

Conservation at a land-interface

\[ \frac{dc}{dt} = \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} + v \frac{\partial c}{\partial y} + w \frac{\partial c}{\partial z} \qquad(3)\]

Keeping track of all four terms can become quite difficult, especially in heterogeneous terrain.

Horizontal Homogeneity

\[ \frac{dc}{dt} = \frac{\partial c}{\partial t} \color{gray}{+ u \frac{\partial c}{\partial x} + v \frac{\partial c}{\partial y}} + w \frac{\partial c}{\partial z} \qquad(4)\]

Over flat, homogeneous ecosystems this task becomes “fairly” simple for most variables:

• The mean horizontal gradients “vanish”

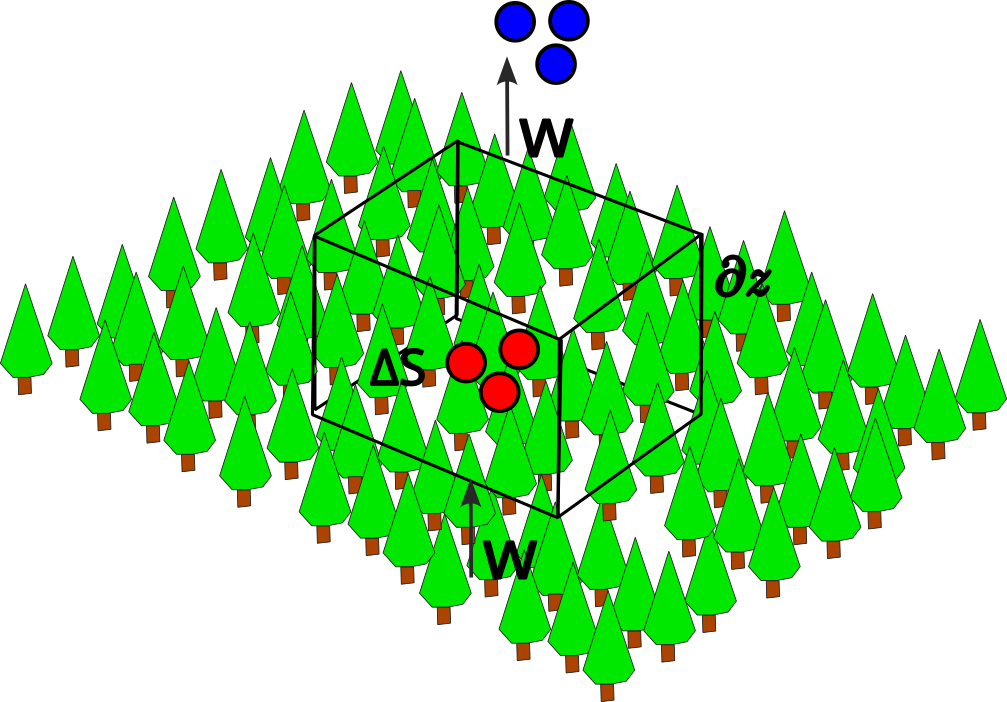
Horizontal Homogeneity

\[ \frac{dc}{dt} = \frac{\partial c}{\partial t} \color{white}{+ u \frac{\partial c}{\partial x} + v \frac{\partial c}{\partial y}} + w \frac{\partial c}{\partial z} \qquad(5)\]

• \(w \frac{\partial \overline{c}}{\partial z} \gg u \frac{\partial \overline{c}}{\partial x} = v \frac{\partial \overline{c}}{\partial y} \approx 0\)

  • Overbar indicates time-average (e.g, an hour)
  • Horizontal transport reduces to zero in homogenous terrain

Horizontal Homogeneity

Reducing to 1D simplifies calculations. We assume horizontal advection on opposite sides of the ‘box’ cancel out. Only vertical exchange is considered.

\[ \frac{dc}{dt} = \frac{\partial c}{\partial t} + w \frac{\partial c}{\partial z} \qquad(6)\]

Making Assumptions

There is a famous saying about assumptions …

• There will always be some heterogeneity present, even in “uniform” ecosystems.
  • But depending on the scale we are concerned with, it is sufficient to “ignore” the small scale variability.

Study Question

Apply the conservation equation to absolute humidity.

Mechanisms of Energy and Mass Transfer

Radiative exchange: electromagnetic waves, photons

• Radiation does not need molecules to propagate, it can travel through the vacuum of space
  • All inputs to / outputs from the Earth system

Mechanisms of Energy and Mass Transfer

Molecular exchange: conduction and diffusion

• Net flow of energy or matter from high concentration to low concentration
  • Heat conduction is most effective in solids, less so in liquids and gasses

Diffusion, process resulting from random motion of molecules by which there is a net flow of matter from a region of high concentration to a region of low concentration. Heat conduction involves thermal energy transported, or diffused, from higher to lower temperature. Heat conduction is usually an effective mode of transfer in solids, less so in liquids, and least important in gases. In general, pure molecular conduction is negligible in atmospheric applications, except within the very think laminar boundary layer. However, conduction is important to the transport of heat beneath the surface. As we’ll get to later in this course, conduction of heat is dependent on the thermal properties of the substrate.

Mechanisms of Energy and Mass Transfer

Turbulent exchange: - convection (bulk transport) in a fluid

• Convection is the most effective mode of transport in the atmosphere. It can be free (self propagating) or forced (mechanically induced).

e.g. looking at boiling water In the atmosphere, the parcels of air (or eddies) transport energy and mass from one location to another. The eddies may be set into turbulent motion by free or forced convection. Free convection is due to the parcel of air being at a different density than the surrounding fluid (e.g. the motion of water in a heated kettle, and a similar bubbling of air parcels occurs when the Earth’s surface is strongly heated by solar radiation). Forced (mechanical) convection – flow of air or water over obstacles. Depends on the roughness of the surface and the speed of the horizontal flow.

Transport of Energy and Mass in the Climate System

Table 1: Examples of processes relevant to the Earth-Climate system.

Method of exchange	Electromagnetic Energy	Heat Energy	Mass
Radiative	Short Wave (\(SW\)) Long Wave (\(LW\)) Net Radiation (\(R_n\))	-	-
Molecular	Electricity conduction (not relevant in the atmosphere)	Heat conduction	Diffusion of water vapour molecules
Turbulent	Turbulent exchange of charged gases (thunderstorms)	Sensible heat flux density	Latent heat flux density

Heat, energy that is transferred from one body to another as the result of a difference in temperature.

Fluxes vs Flux Densities

Energy: Radiant or heat energy, given in Joules (\(\rm{J}\)), describes the total energy in system

Power: Radiant or heat flux, given in Watts (\(\rm{W}=\rm{J}\rm{s^{-1}}\)), describes the flow rate of energy.

Flux Density: Radiant or heat flux density, given in Watts per unit area (\(\rm{W}\rm{m^{-2}}\)), describes flow of energy across a surface.

Energy is the quantitative property that must be transferred to an object in order to perform work on, or to heat, the object Common forms of energy include the kinetic energy of a moving object, the potential energy stored by an object’s position in a force field (gravitational, electric or magnetic), the radiant energy carried by light, and the thermal energy due to an object’s temperature (the elastic energy stored by stretching solid objects, the chemical energy released when a fuel burns)

power is the rate of doing work or transferring heat (i.e. the amount of energy transferred or converted per unit time) power is energy divided by time

Flux Densities

Flux densities can be calculated for any property, just be mindful of the units.

Mass: (\(\rm{kg}\rm{m^{-2}}\))

Heat: (\(\rm{W}\rm{m^{-2}}\))

Radiation: (\(\rm{W}\rm{m^{-2}}\))

Energy is the quantitative property that must be transferred to an object in order to perform work on, or to heat, the object Common forms of energy include the kinetic energy of a moving object, the potential energy stored by an object’s position in a force field (gravitational, electric or magnetic), the radiant energy carried by light, and the thermal energy due to an object’s temperature (the elastic energy stored by stretching solid objects, the chemical energy released when a fuel burns)

power is the rate of doing work or transferring heat (i.e. the amount of energy transferred or converted per unit time) power is energy divided by time

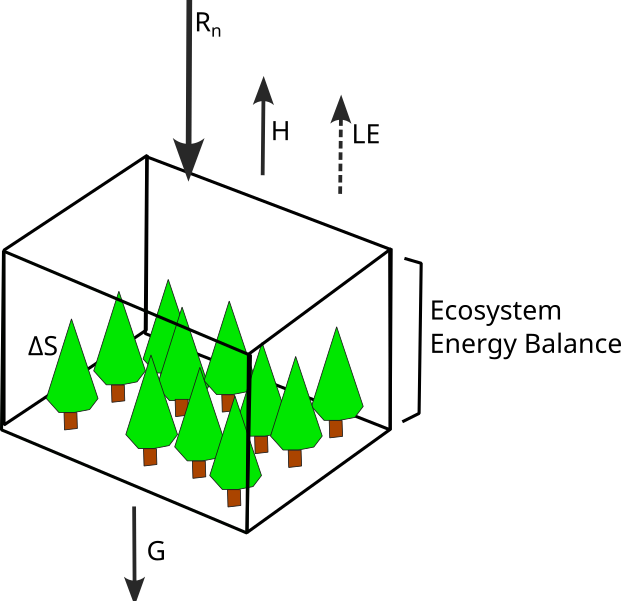
Energy Fluxes at Earth’s Surface

\[ R_n = H + LE + G + \Delta S \qquad(7)\]

• ‘Ideal’ surface considered here is relatively smooth, horizontal, homogeneous, extensive, and opaque to radiation.
• Only vertical fluxes need to be considered.

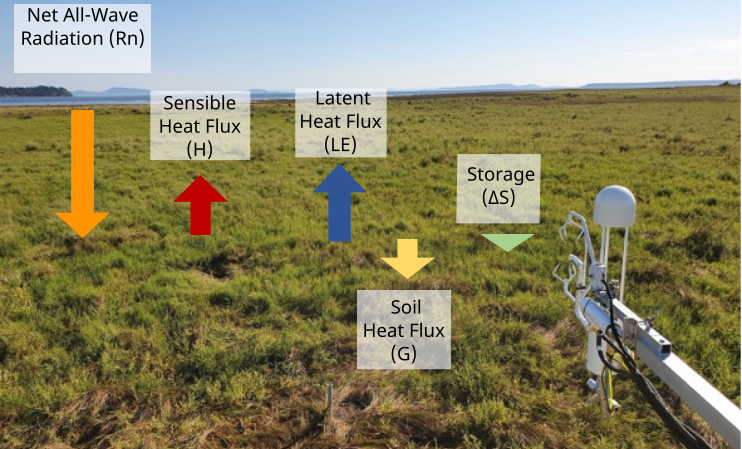
Net Radiation (\(R_n\))

The net radiative flux is a result of the radiation balance at the surface, which will be discussed in more detail in a few lectures.

• Daytime dominated by the solar radiation (toward the surface), at night the net radiation is much weaker & away from the surface.
  • The surface warms up during the daytime, while it cools during the evening and night hours.

Sensible vs. Latent Heat (iClicker)

One component deals with heat energy we can feel, the other deals with heat energy that is “hidden”. Which component is describes that hidden heat energy?

• Sensible Heat Flux
• Latent Heat Flux

Sensible Heat Flux (\(H\))

A result of the difference in the temperatures of the surface and the air above.

• In the bottom few millimeters of the air, conduction is the primary mode of heat transfer.

• Above this, advection or convection involving air motions become dominant.

• The sensible heat flux is usually directed away from the surface during the daytime hours, when the surface is warmer than the air above, and vice versa during the evening and nighttime periods.

Latent Heat Flux (\(LE\))

A result of the energy exchange associated with phase changes (evaporation, condensation, etc.) at the surface.

• Evaporation results in some cooling of the surface, and transfer of heat energy from the surface to the air above.
  • The opposite is true for condensation.

Ground Heat Flux (\(G\))

Heat exchange through the ground is primarily due to conduction if the medium is soil, rock, or concrete. Through water, advection or convection are also significant.

• The depth of the medium which responds to changes in the energy fluxes at the surface on a diurnal basis, is typically < 1 m for land surfaces and < 50 m for lakes and oceans.

Storage (\(\Delta S\))

Storage is a catch all term that can include many different components deponing on the context.

• Photosynthesis is a good example when dealing with vegetated surfaces. On a sunny day, a portion of the \(R_n\) is converted to chemical potential energy and stored in the ecosystem for later use.
  • This can give the appearance of an imbalance in the energy budget if photosynthesis is not monitored.

Take home points

• We discussed the conservation of energy and mass as a powerful principle to describe exchange in the atmosphere.
• Transfer of mass and energy (heat and radiant energy) can be quantified using flux densities, where transfer is normalized per unit area and unit time.
• We introduced the surface energy balance for an ideal surface.